Re: Year 11 Mathematics 3 Unit Cambridge Question & Answer Thread
Question 18 a and c from 6A:
Simplify:
a)
 + 2})
the denominator is meant to be 2^n+1 +2, can't get it to work for some reason.
answer is :
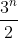
c)
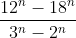
answer is: -2^n3^n
To write
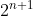
, the LaTeX code needs to be written like this: 2^{n+1} (put curly braces around the thing you want in the exponent).
Part a)
Based on what you say the answer is, I think you made a typo in the numerator, it should be
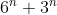
instead (OR, the denominator should be
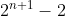
. I'll assume the numerator is
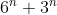
.
Then the numerator can be written as:
^n + 3^n)
(as
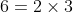
)
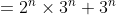
(using the index law
^n = a^n \times b^n)
)
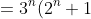)
(factorising).
The denominator
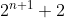
can be written as:
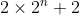
(as
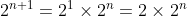
, using the index law

)
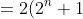)
(factorising).
So the original fraction is
}{2(2^n + 1)}=\frac{3^n}{2})
(cancelling
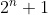
).
Part c)
The idea is to rewrite the numerator in terms of
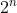
and
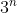
using index laws, and then hopefully we will be able to cancel something with the denominator (notice that 12 and 18 can both be written in terms of powers of 2 and 3).
The numerator
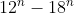
can be written as:
^n - \left(2\times 3^2\right)^n)
(as
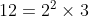
and
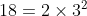
)
^n \times 3^n - 2^n \times \left(3^2 \right)^n )
(using the index law
^n = a^n \times b^n)
)
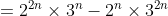
(using the index law
^n = a^{bn})
)
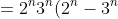)
(factorising by taking out a common factor of
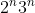
)
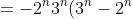)
(as
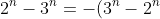)
).
So the original fraction becomes
}{3^n - 2^n}=-2^n 3^n\text{ }(=-6^n))
.
