-
Looking for HSC notes and resources? Check out our Notes & Resources page
combinations ext math question (1 Viewer)
- Thread starter qwerla
- Start date
the answer is 13860What's the answer? I haven't done perms and combs in a while but my guess is (12C6)5!*(6C4)3!*(2C2)1! = 9979200.
- Joined
- Feb 16, 2005
- Messages
- 8,139
- Gender
- Male
- HSC
- 2006
Do it sequentially:
- There are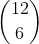 ways to select 12 people to form the table of 6
ways to select 12 people to form the table of 6
- Once those 6 are selected there are 6 left so there are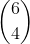 ways to select 6 people to form the table of 4
ways to select 6 people to form the table of 4
- Once those 4 are selected there are 2 left so there is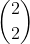 way to form the table of 2
way to form the table of 2
As these events occur simultaneously, the product of these gives your answer. You’ll get the same answer regardless of which table you start with first.
- There are
- Once those 6 are selected there are 6 left so there are
- Once those 4 are selected there are 2 left so there is
As these events occur simultaneously, the product of these gives your answer. You’ll get the same answer regardless of which table you start with first.
hey!!! thank you SO much! this makes sm sense to me now, and thank you so much for the picture above. it really clarified it for me. hope u have a great rest of ur dayView attachment 30620
this is in my y11 notes haha
in this case we would have
as seen in the last formula
hope this helps!
thank you very much!!Do it sequentially:
- There areways to select 12 people to form the table of 6
- Once those 6 are selected there are 6 left so there areways to select 6 people to form the table of 4
- Once those 4 are selected there are 2 left so there isway to form the table of 2
As these events occur simultaneously, the product of these gives your answer. You’ll get the same answer regardless of which table you start with first.

