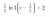Hi guys,
I need some help on a couple of questions:
1. Find the equation if f(x)=1/3 x^3 is translated horizontally 1/2 units to the right.
Why is the answer 1/2(2x-1)^3 instead of 1/3(x-1/2)^3? What are the differences?
2. f(x)=ln x has a vertical translation of 2 upwards and vertical dilation with factor 1/2, a horizontally dilation with factor 3 and a horizontal translation of 1/5 to the right.
Up until the last transformation, I've got 1/2 ln 3x+2, how do I show the final horizontal translation of 1/5?
Thanks guys!
I need some help on a couple of questions:
1. Find the equation if f(x)=1/3 x^3 is translated horizontally 1/2 units to the right.
Why is the answer 1/2(2x-1)^3 instead of 1/3(x-1/2)^3? What are the differences?
2. f(x)=ln x has a vertical translation of 2 upwards and vertical dilation with factor 1/2, a horizontally dilation with factor 3 and a horizontal translation of 1/5 to the right.
Up until the last transformation, I've got 1/2 ln 3x+2, how do I show the final horizontal translation of 1/5?
Thanks guys!