Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
DMT (de moive's theorem) q. (1 Viewer)
- Thread starter astj
- Start date
I think what is going on they are applying binomial theorem.View attachment 42144
I've converted 1+i and 1-i into mod-arg form and subbed the n in but I don't know how to get the RHS as well as part ii. Thanks in advance
Basically you should try expand (1+i)^n and (1-i)^n.
I will need to double check to make sure.
WeiWeiMan
Well-Known Member
1+i=√2cisπ/4View attachment 42144
I've converted 1+i and 1-i into mod-arg form and subbed the n in but I don't know how to get the RHS as well as part ii. Thanks in advance
1-i = √2cis(-π/4)
(√2cisπ/4)^n+(√2cis(-π/4))^n
= √2^n (cis(nπ/4)+cis(-nπ/4))
=2(√2)^n cos(nπ/4) QED as req blah blah blah
for part ii do as cossine said (use binomial expansion) and see what happens
okk cool thanks, how would you do part ii then?1+i=√2cisπ/4
1-i = √2cis(-π/4)
(√2cisπ/4)^n+(√2cis(-π/4))^n
= √2^n (cis(nπ/4)+cis(-nπ/4))
=2(√2)^n cos(nπ/4) QED as req blah blah blah
for part ii do as cossine said (use binomial expansion) and see what happens
part ii)
The question states that we should use the result from part i. Lets use the statement that n is divisible by 4, that is we suppose that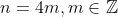 .
.
Then we put that into the result from part i,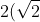^{4m}\cos(m\pi)=2(\sqrt{2})^{4m}(-1)^{m}) convert it back into terms of n,
convert it back into terms of n, 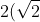^{n}(-1)^{\frac{n}{4}}) .
.
Now the LHS of that question contains a bunch of n choose expressions, which suggests binomial expansion, so we will expand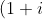^n+(1-i)^n\\\\={n \choose 0}+i{n \choose 1}-{n \choose 2}-i{n \choose 3}+{n \choose 4}+...+{n \choose n}+{n \choose 0}-i{n \choose 1}-{n \choose 2}+i{n \choose 3}+{n \choose 4}+...+{n \choose n})
which simplifies to)
now equating these two new expressions gives us the answer.
The question states that we should use the result from part i. Lets use the statement that n is divisible by 4, that is we suppose that
Then we put that into the result from part i,
Now the LHS of that question contains a bunch of n choose expressions, which suggests binomial expansion, so we will expand
which simplifies to
now equating these two new expressions gives us the answer.


