Yep, it's
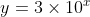
. Here's a way to derive it:
The "
y-axis", corresponds to the following: going up a physical distance of
d units on the
y-axis represents the value
y = 10
d. So
d = log
10 y, where
y is the reading on the
y-axis when you go up
d units.
The slope of the line is
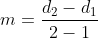
, where

is the distance along the
y-axis at
x = 2 (which is log
300, as
y = 300 here) and
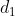
is the distance along the
y-axis at
x = 1 (which is log
10 30, as
y = 30 here). (Note that the
x-axis is linear and 1:1 scale, i.e. a distance of
d along it represents a value of
d for
x, which is why the denominator in the slope formula is just
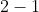
.)
So the slope of this straight line is
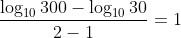
(using log laws to simplify).
So the equation of the straight line is
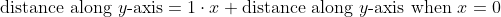
(this is just slope-intercept form of a straight line when the axes are to scale, i.e. a distance of
d along each axis represents a value of
d of that variable).
i.e.
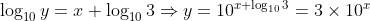
(using log laws and index laws).
