In many 4U exam papers I have come across, there will usually be a question that goes like:
Prove
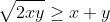
Keep in mind the question might ask for something that looks different (but in essence is the same) such as: Prove

Both proofs I would recommend a "backwards reasoning" method. I like this method because it's quick, and it's easy to remember once you've done it a couple of times. For backwards reasoning, usually your first step is one that is hard to ascertain:
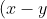^2\geq0)
OR
^2\geq0)
Then expand to get:
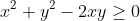
OR

Rearrange the inequalities to get your answer. And the proof is then complete (feel free to write QED or #, though this isn't necessary from my experience).
You will also encounter questions that will require you to substitute variables into this basic AM/GM inequality. Take a look at Question 15 (a) (i) of the 2021 HSC 4U paper:
We are given
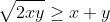
and are required to show (for non-negative real numbers)

Substitutions would be required. In this case, we would let
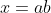
and

The rest of the solution would go as such:
View attachment 34854
There are other substitutions you could have made, but this is the simplest.
Practice lots of questions, and you will see what sort of substitutions you will have to make. You should be also able to identify which questions ask for use of the AM/GM inequality.