-
Finished your HSC? Check out our University Discussion, Non-School forums or help out next year's HSC students! -
YOU can help the next generation of students in the community! Share your trial papers and notes on our Notes & Resources page
Hard differentiation (1 Viewer)
- Thread starter Bdogz
- Start date
the-derivative
BCom/LLB (UNSW)
- Joined
- Nov 11, 2007
- Messages
- 2,124
- Gender
- Male
- HSC
- 2009
Let dy/dx = y'
Therefore the derivative with respect to x of ln (y-x) would be:
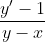
Therefore the derivative with respect to x of ln (y-x) would be:
oh k so wat wud be the derivative with respect to x of this equation : y=x^siny + xLet dy/dx = y'
Therefore the derivative with respect to x of ln (y-x) would be:
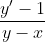
i got 2 this step but im nto sure how much of it is right: dy/dx=(lnx.cosy.dy/dx + siny.1/x).e^sinylnx + 1
Last edited:
its a completely different question to the 1st thing i posted on here sorry, so the question is find dy/dx of y=x^siny + xis that y = x^siny + x or z= x^siny + x?
if the latter, dz/dx = x^sin(y)*sin(y)/x+1
Pwnage101
Moderator
-1/ln(y-x)
you treat the y as a constant.
Functions of several vairables is not in the HSC, hence partial derivatives is beyond the scope of the syllabus.is that y = x^siny + x or z= x^siny + x?
if the latter, dz/dx = x^sin(y)*sin(y)/x+1
on the bottom line in denominator i got cosy instead of cosx, but apart from that i got wat u got, i dont hv the answer on me but once i get it ill notify u thanksIs it: y = xsin y + x ??
If so, is the answer ??
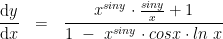
NB i shudve put this in the tertiary forum sorry
Last edited:
-Onlooker-
Member
- Joined
- Mar 15, 2009
- Messages
- 150
- Gender
- Male
- HSC
- 2009
Functions of several vairables is not in the HSC, hence partial derivatives is beyond the scope of the syllabus.
You sure?
iirc; one of the hsc papers asked us to differentiate or integrate cos (x - y ). It was in the earlier years.
edit: It might not have asked us directly; might have been in the solutions, I can't remember 100% sorry.
This is the answer thanksIs it: y = xsin y + x ??
If so, is the answer ??
Edit: corrected: it's cos y not cos x; my typo.

