Hard Questions (3 Viewers)

[KingOfActing]

Yeah. Well that's hard. But jokes aside, do you know that the Riemann Zeta function WAS actually examined in the HSC in 1975? So here is a not-so-hard question - HSC 1975 4 unit Q9i:



See if you can do it.

 

[KingOfActing]

The infinite sum is a first-order linear approximation of the following integral:



Two approximations are constructed such that they are definitively greater and lesser than the true value of the integral. Since the integral only converges for s>1, it follows that the sum only converges for s>1. QED.

This isn't a formal proof, strictly speaking, but I cbbs rn. I'll come back to patch it up later.

Your way works, just evaluate the integral:



So by the integral convergence test, the series converges for s > 1

 

[parad0xica]

and also this one about counting technique:

How many whole numbers from 1000 to 9999 have 6 as the sum of their digits?

Bump

 

[Paradoxica]

Nice.

Although mathematically speaking, the two methods are identical, yours is a lot faster.

 

[KingOfActing]

Bump

Let D(a,b) be the number of ways to make a sum of a with b numbers.

Let our number be of the form A|B|C|D|

A can take the values 1-6

D(a,b) can take the following recurrence:

D(0,b) = 1
D(1,b) = b
D(a,1) = 1
D(a, b) = Sum n=0 to a D(n, b - 1)


It is simple to see D(a,b) = D(a-1,b) + D(a,b-1) I think that's wrong

Our sum is D(6,4) - D(6,3) (since the first digit can't be 0). Using the recurrence relation:
D(0,3) + D(1,3) + D(2,3) + D(3,3) + D(4,3) + D(5,3) = 4 + 4D(2,2) + 4D(1,2) + 4D(0,2) + 3D(3,2) + 2D(4,2) + D(5,2) = ... = 56

Hopefully right the second time, I keep making calc mistakes

 

[Paradoxica]

and also this one about counting technique:

How many whole numbers from 1000 to 9999 have 6 as the sum of their digits?

It is obvious none of the digits can be greater than 6.

So the desired integers lie between 1000 and 6000.

For the 5000's, any number greater than 5100 immediately fails.

repeating the arguments over all the thousands, we have the following intervals to analyse:

1000<=n<=1500

2000<=n<=2400

3000<=n<=3300

4000<=n<=4200

5000<=n<=5100

6000<=n<=um.

Case bash the remaining intervals in a similar fashion.

cbbs.

 

[RealiseNothing]

and also this one about counting technique:

How many whole numbers from 1000 to 9999 have 6 as the sum of their digits?

Since the sum of the digits must be 6, we can write it as:

1_1_1_1_1_1_

Just use the stars and bars method, since we need to put in 3 bars to represent the digits. So we get

i.e. 1_1 | 1_1 | 1 | 1 = 2211

 

[Paradoxica]

Since the sum of the digits must be 6, we can write it as:

1_1_1_1_1_1_

Just use the stars and bars method, since we need to put in 3 bars to represent the digits. So we get

i.e. 1_1 | 1_1 | 1 | 1 = 2211

Although the idea is good, I think the answer is not that, since multiple bars can exist next to each other

 

[Drongoski]

Since the sum of the digits must be 6, we can write it as:

1_1_1_1_1_1_

Just use the stars and bars method, since we need to put in 3 bars to represent the digits. So we get

i.e. 1_1 | 1_1 | 1 | 1 = 2211

56 is also what I got.

The stars & bars method was pioneered by William Feller in his book: An Introduction to Probability Theory

 

[dan964]

I have discovered a truly marvellous proof of this, which this post is too small to contain.

tywebb's site has a proof of Fermat's Theorem. I don't quite get it. But it is still fascinating.

 

[seanieg89]

tywebb's site has a proof of Fermat's Theorem. I don't quite get it. But it is still fascinating.

Quite a lot of background is needed to understand Wiles' proof at any greater depth than the absolute "top level overview".

 

[RealiseNothing]

Although the idea is good, I think the answer is not that, since multiple bars can exist next to each other

My method allows for that (56 is most definitely correct).

 

[dan964]

1. By considering the cross-sections of the figure, sketch

2. If show that



Note I am using older notation here (edit here is the equivalent notation)

 

[Carrotsticks]

1. By considering the cross-sections of the figure, sketch

2. If show that



Note I am using older notation here (edit here is the equivalent notation)

OP is a Year 12 student Extension 1. These are not in the scope of the HSC syllabus.

Also, these aren't particularly difficult problems. I am almost certain that my Year 11 class, who just learned Chain Rule less than a week ago, could do the second problem, given a 30 second introduction on how to compute partials.

 

[KingOfActing]

1. By considering the cross-sections of the figure, sketch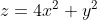

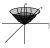
Well, it is clear z > 0. By setting z to 1 (or any other positive constant), it's clear that the horizontal cross-section is that of an ellipse, which is stretched with major axis being the y-axis. By considering y or x being constant, it is clear the shape traced is that of a parabola. Hence the shape is an "elliptic paraboloid" (is that the right term?). Basically it's like a 3-d parabola that's stretched on the y-axis.

masterful paint skills

 

[Nailgun]

Well, it is clear z > 0. By setting z to 1 (or any other positive constant), it's clear that the horizontal cross-section is that of an ellipse, which is stretched with major axis being the y-axis. By considering y or x being constant, it is clear the shape traced is that of a parabola. Hence the shape is an "elliptic paraboloid" (is that the right term?). Basically it's like a 3-d parabola that's stretched on the y-axis.

masterful paint skills View attachment 33073

wow thats actually pree impressive paint skills lol

would rep but

"You must spread some Reputation around before giving it to KingOfActing again."

 

[KingOfActing]

wow thats actually pree impressive paint skills lol

would rep but

"You must spread some Reputation around before giving it to KingOfActing again."

thanks man

feeling the love

 

[wu345]

 

[KINGOM 885]

View attachment 33077

Nice Question

 

[Paradoxica]

Here's a funny one from Fort Street Leaving Certificate trial 1959 Question 3a:

Differentiate x^xx

Trivial by inspection.