AbsoluteValue
Member
The AM-GM inequality states that for any n positive real numbers a1, a2, a3, … an:
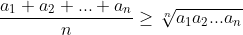
Prove that:
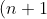^n\geq%202^{n}n!)
Can anyone prove this? It is really tricky but once you get it is easy to solve.
Prove that:
Can anyone prove this? It is really tricky but once you get it is easy to solve.
Last edited:
