Help with polynomials question (1 Viewer)

[Bob_man]

I'm having some trouble getting the answer for question 7b.

 

[jks22]

I'm having some trouble getting the answer for question 7b. View attachment 34901View attachment 34902

I'd just use long division to find the solutions

x^4-10x^3+34x^2-42x+9 divided by x-3 = x^3-7x^2+13x-3

x^4-10x^3+34x^2-42x+9 = (x-3)(x^3-7x^2+13x-3) = 0

Let P(x) = x^3-7x^2+13x-3

P(3) = 0, thus x-3 is a factor

x^3-7x^2+13x-3 divided by x-3 = x^2-4x+1

x^3-7x^2+13x-3 = (x-3)(x^2-4x+1)

Thus x^4-10x^3+34x^2-42x+9 = (x-3)(x-3)(x^2-4x+1) = 0

So x = 3 and then solve for x^2-4x+1 = 0

 

[5uckerberg]

I'm having some trouble getting the answer for question 7b. View attachment 34901View attachment 34902

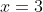
Let me ask you a question, what do you know if is a double root of the equation?
If that is the case then you can have is a root of the equation.
Now you have this in the net we can now have

What do we have here?
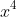
We want as the leading pronumeral so now we will have

Next, you have to take into account that you have
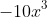
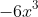
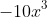
We already have from the previous step so how do we get . Take away .
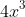
As such we have
To make your life easier instead of going for the x squared term or the x term we are finding the constant.
So in this case 9 times what gives 9. The answer is simply 1.
There we have
Now you can do whatever you want with to find the factors and as such it will give you the answer that you have shown us.

 

[5uckerberg]

From this question you can also have



Simplifying gives



To find the roots instead of focusing on the product of roots let's have a look at the sum of roots. You see how the sum of roots is 4 right.
Well note that is a parabola and parabolas are symmetric.

In this case differentiate twice to determine the minimum turning point which if the hard work is done will give you 2. Now remember how I said the parabola has a symmetric property well in this case now we focus on the product of roots which will then give us




There your roots are