Let
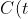)
be the concentration of the chemical at time
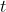
weeks after the discovery of the dumping. Let
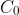
be the concentration at the time of the dumping, which occurred at some time
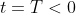
. We know that the concentration of the chemical decays according to the equation
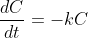
for some constant
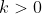
and the solution of this differential equation is
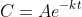
for some constant
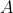
. We know that the concentration has fallen from
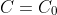
at time
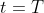
to
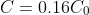
at time
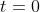
and to
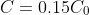
at time
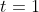
. Using the latter two pieces of information, we get
)
and
)
Dividing equation (1) by equation (2) yields
 \end{align*})
So, we can find
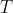
, where
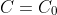
:
} \\ \frac{C_0}{0.16C_0} &= e^{-kT} \\ 0.16 &= e^{kT} \\ \ln{0.16} &= kT \\ \ln\left(\frac{4}{25}\right) &= T\ln\left(\frac{16}{15}\right) \\ T &= \frac{\ln{4} - \ln{25}}{\ln{16}-\ln{15}} \\ &= \frac{2\ln{2} - 2\ln{5}}{4\ln{2}-\ln{15}} \\ &= -28.395... \\ &\approx\ \text{28 weeks and 3 days prior to $t = 0$} \end{align*})
So, based on decay rates, the contamination / dumping occurred 28 weeks and 3 days prior to it being discovered.
Suspect A was imprisoned for 26 weeks ending 1 week prior to the discovery, and so was imprisoned 27 weeks prior to the discovery of the contamination, and so was free at the time the dumping occurred.
Suspect B was imprisoned for 26 weeks ending 13 weeks prior to the discovery, and so was imprisoned at 39 weeks prior to the discovery and was still imprisoned when the dumping occurred.
The contamination decay rates are consistent with Suspect A being free at the time the crime was committed but Suspect B being incarcerated at that time and so unable to commit the crime. Based on these results, Suspect B is innocent and Suspect A remains under suspicion and is potentially the offender.

