miniwaybzz
Member
- Joined
- Sep 14, 2010
- Messages
- 85
- Gender
- Male
- HSC
- N/A
hey guys,
can anyone help me with the 05 paper Q6)iii) [FML stuck on a q6 question ]
]
V = 3600 ( 1 - t/60 ) ^2 where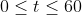
At what time does the model predict that the water will drain from the
tank at its fastest rate?
How do we approach this? fastest rate? so since rate = first derivative , we find 2nd derivative for maximum ? :S
thanks
can anyone help me with the 05 paper Q6)iii) [FML stuck on a q6 question
V = 3600 ( 1 - t/60 ) ^2 where
At what time does the model predict that the water will drain from the
tank at its fastest rate?
How do we approach this? fastest rate? so since rate = first derivative , we find 2nd derivative for maximum ? :S
thanks
