HSC 2013-14 MX1 Marathon (archive) (3 Viewers)

seanieg89 · May 23, 2013

Re: HSC 2013 3U Marathon Thread

And these sort of expressions are usually integrated by cases.

RealiseNothing · May 23, 2013

Re: HSC 2013 3U Marathon Thread

seanieg89 said:
The insides being trigonometric has nothing to do with it, it is just that

$\sqrt{u^2}=|u|$ .

Is there anything you can do to get around this or compensate for the extra positive area you get?

RealiseNothing · May 23, 2013

Re: HSC 2013 3U Marathon Thread

Show that:

$\frac{\pi}{2} > \lim_{\alpha \to 1} \int_{0}^{\alpha} \sqrt{1+x^2+x^4+...+x^{2n}}~dx > 1$

seanieg89 · May 23, 2013

Re: HSC 2013 3U Marathon Thread

Yeah, you can use floor functions to find an expression for the DEFINITE integral between 0 and a for an arbitrary a. Let this expression be F(a), extend it to the whole real line by asserting that it must be odd, and add an arbitrary constant. This will be a primitive valid over the real line.

anomalousdecay · May 23, 2013

Re: HSC 2013 3U Marathon Thread

I was in 2-unit one day and discovered a new way to use Newton's method of approximation, to get an exact answer of something.
How ironic, using an approximation to get the exact answer.
This is only a 2-unit question, but by being limited to using Newton's method of Approximation, it becomes extension 1 work.

Given that the curve is y=x^2, find the equation of the tangent, given it touches y = x^2 at point A.

Hence, find the x-value of the intersection of the tangent with the curve, given that the tangent touches the x-axis at x=2, Using only Newton's approximation method (You must use it because I am a harsh marker)

I discovered this result on my own, hopefully you guys can too. Image made using Geogebra.

nightweaver066 · May 23, 2013

Re: HSC 2013 3U Marathon Thread

$\int \frac{1}{\sqrt{4x^2+4x+5}}dx$

RealiseNothing · May 23, 2013

Re: HSC 2013 3U Marathon Thread

anomalousdecay said:
I was in 2-unit one day and discovered a new way to use Newton's method of approximation, to get an exact answer of something.
How ironic, using an approximation to get the exact answer.
This is only a 2-unit question, but by being limited to using Newton's method of Approximation, it becomes extension 1 work.

View attachment 28150
Given that the curve is y=x^2, find the equation of the tangent, given it touches y = x^2 at point A.

Hence, find the x-value of the intersection of the tangent with the curve, given that the tangent touches the x-axis at x=2, Using only Newton's approximation method (You must use it because I am a harsh marker)

I discovered this result on my own, hopefully you guys can too. Image made using Geogebra.

Isn't this essentially the proof of Newton's method but working backwards?

RealiseNothing · May 23, 2013

Re: HSC 2013 3U Marathon Thread

i.e. we want to find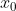 $x_0$

$x_1 = x_0 - \frac{f(x_0)}{f'(x_0)}$

$x_0 = x_1 + \frac{f(x_0)}{f'(x_0)}$

$x_0 = 2 + \frac{x_0^2}{2x_0}$

$2x_0 = 4 + x_0$

$x_0 = 4$

Makematics · May 24, 2013

Re: HSC 2013 3U Marathon Thread

Sy123 said:
That isn't correct.

after checking the answer using 3 different methods, i can confirm it is indeed correct. well technically there are two answers if you take different cases, but sqrt (1+sin2x) +c is one of them at least

if you change 1+sin2x into sin ^2 x +cos ^2 x + 2sinxcosx, it becomes sinx + cosx +c, which is the simplified answer.

Sy123 · May 24, 2013

Re: HSC 2013 3U Marathon Thread

Makematics said:
after checking the answer using 3 different methods, i can confirm it is indeed correct. well technically there are two answers if you take different cases, but sqrt (1+sin2x) +c is one of them at least if you change 1+sin2x into sin ^2 x +cos ^2 x + 2sinxcosx, it becomes sinx + cosx +c, which is the simplified answer.

My mistake

anomalousdecay · May 24, 2013

Re: HSC 2013 3U Marathon Thread

RealiseNothing said:
Isn't this essentially the proof of Newton's method but working backwards?

i.e. we want to find $x_0$

$x_1 = x_0 - \frac{f(x_0)}{f'(x_0)}$

$x_0 = x_1 + \frac{f(x_0)}{f'(x_0)}$

$x_0 = 2 + \frac{x_0^2}{2x_0}$

$2x_0 = 4 + x_0$

$x_0 = 4$

That's correct. Well done.

It is similar to the proof, but it doesn't actually prove it, unless you already have $x_o = 4$ in teh question.

But I just found it interesting and a much more elegant way of answering the question. I did that in my 2-unit exam, because I got bored with the extra time.

anomalousdecay · May 24, 2013

Re: HSC 2013 3U Marathon Thread

RealiseNothing said:
Isn't this essentially the proof of Newton's method but working backwards?

i.e. we want to find $x_0$

$x_1 = x_0 - \frac{f(x_0)}{f'(x_0)}$

$x_0 = x_1 + \frac{f(x_0)}{f'(x_0)}$

$x_0 = 2 + \frac{x_0^2}{2x_0}$

$2x_0 = 4 + x_0$

$x_0 = 4$

That's correct. Well done.

It is similar to the proof, but it doesn't actually prove it, unless you already have $x_o = 4$ in the question.

But I just found it interesting and a much more elegant way of answering the question. I did that in my 2-unit exam, because I got bored with the extra time.

Sy123 · Jun 6, 2013

Re: HSC 2013 3U Marathon Thread

$\int_0^{2\pi} \sqrt{1-\cos^2 x} \ dx$

HeroicPandas · Jun 6, 2013

Re: HSC 2013 3U Marathon Thread

Sy123 said:
$\int_0^{2\pi} \sqrt{1-\cos^2 x} \ dx$

$$Let I = $\int_0^{2\pi} \sqrt{1-\cos^2 x} \ dx \\ I = \int_0^{2\pi}|sinx|dx \\ \\I = \int_0^{\frac{\pi}{2}}|sinx|dx + \int_{\frac{\pi}{2}}^{\pi}|sinx|dx + \int_{\pi}^{\frac{3\pi}{2}} |sinx|dx + \int_{\frac{3\pi}{2}}^{2\pi}|sinx|dx \\ A.T.S.C ($A turtle seeking corn) \\ \\ \therefore I = $\int_0^{\frac{\pi}{2}}sinxdx + \int_{\frac{\pi}{2}}^{\pi}sinxdx - \int_{\pi}^{\frac{3\pi}{2}} sinxdx - \int_{\frac{3\pi}{2}}^{2\pi}sinxdx \\ \\ \therefore I = 1+ \dots $By inspection areas under curve blah blah \\ \therefore I = 1+1-1-1 = 0$

i dont need to put absolute because its not area yeh?

Sy123 · Jun 6, 2013

Re: HSC 2013 3U Marathon Thread

HeroicPandas said:
$$Let I = $\int_0^{2\pi} \sqrt{1-\cos^2 x} \ dx \\ I = \int_0^{2\pi}|sinx|dx \\ \\I = \int_0^{\frac{\pi}{2}}|sinx|dx + \int_{\frac{\pi}{2}}^{\pi}|sinx|dx + \int_{\pi}^{\frac{3\pi}{2}} |sinx|dx + \int_{\frac{3\pi}{2}}^{2\pi}|sinx|dx \\ A.T.S.C ($A turtle seeking corn) \\ \\ \therefore I = $\int_0^{\frac{\pi}{2}}sinxdx + \int_{\frac{\pi}{2}}^{\pi}sinxdx - \int_{\pi}^{\frac{3\pi}{2}} sinxdx - \int_{\frac{3\pi}{2}}^{2\pi}sinxdx \\ \\ \therefore I = 1+ \dots $By inspection areas under curve blah blah \\ \therefore I = 1+1-1-1 = 0$

i dont need to put absolute because its not area yeh?

Nope the absolute value needs to be there, and you did the right thing by splitting into 4 integrals (only 2 is needed though).

$\int_{\pi}^{2\pi} |\sin x| \ dx \neq \int_{\pi}^{2\pi} \sin x \ dx$

HeroicPandas · Jun 6, 2013

Re: HSC 2013 3U Marathon Thread

Sy123 said:
Nope the absolute value needs to be there, and you did the right thing by splitting into 4 integrals (only 2 is needed though).

$\int_{\pi}^{2\pi} |\sin x| \ dx \neq \int_{\pi}^{2\pi} \sin x \ dx$

Sorry i wasnt specific

Pretend, I = Z

Split 4 times,

I = |A|+ |B| + |C| + |D|

I = A + B + |- C - D| (i was talking about these absolute values)

i can eliminate each absolute value from each (sinx) because of ASTC

For, 0 ≤x≤ pi/2, sinx >0 (A)
For, pi/2 ≤ x ≤ pi, sinx >0 (S)
For, pi ≤ x ≤ 3pi/2, sinx <0 (T)
For, 3pi/2 ≤ x ≤ 2pi, sinx <0 (C)

and i realised i shouldnt have splitted it into 4 lol

$I = \int_0^{2\pi}|sinx|dx \\ \\ =\int_0^{\pi}sinxdx - \int_{\pi}^{2\pi}sinx.dx ($as sinx is positive in 1st and 2nd quad and negative in the 3rd and 4th quad) \\ = 0$
what abotu this?

Sy123 · Jun 6, 2013

Re: HSC 2013 3U Marathon Thread

HeroicPandas said:
Sorry i wasnt specific

Pretend, I = Z

Split 4 times,

I = |A|+ |B| + |C| + |D|

I = A + B + |- C - D| (i was talking about these absolute values)

i can eliminate each absolute value from each (sinx) because of ASTC

For, 0 ≤x≤ pi/2, sinx >0 (A)
For, pi/2 ≤ x ≤ pi, sinx >0 (S)
For, pi ≤ x ≤ 3pi/2, sinx <0 (T)
For, 3pi/2 ≤ x ≤ 2pi, sinx <0 (C)

and i realised i shouldnt have splitted it into 4 lol

$I = \int_0^{2\pi}|sinx|dx \\ \\ =\int_0^{\pi}sinxdx - \int_{\pi}^{2\pi}sinx.dx ($as sinx is positive in 1st and 2nd quad and negative in the 3rd and 4th quad) \\ = 0$
what abotu this?

Yep and $\int_{\pi}^{2\pi} \sin x = - 1$

So the answer should be 2

asianese · Jun 6, 2013

Re: HSC 2013 3U Marathon Thread

Or just draw a picture lol

twinklegal19 · Jun 6, 2013

Re: HSC 2013 3U Marathon Thread

asianese said:
Or just draw a picture lol

this lol

Sy123 · Jun 9, 2013

Re: HSC 2013 3U Marathon Thread

$Find the value of the sum, where$ \ \ n \ \ $is an integer$

$\tan^{-1} \frac{1}{n} + \dots + \tan^{-1} \frac{1}{3} + \tan^{-1}\frac{1}{2} + \tan^{-1} 1 + \tan^{-1} 2 + \tan^{-1} 3 + \dots + \tan^{-1} n$

HSC 2013-14 MX1 Marathon (archive) (3 Viewers)

Well-Known Member

what is that?It is Cowpea

what is that?It is Cowpea

Well-Known Member

Premium Member

Well-Known Member

what is that?It is Cowpea

what is that?It is Cowpea

Well-Known Member

This too shall pass

Premium Member

Premium Member

This too shall pass

Heroic!

This too shall pass

Heroic!

This too shall pass

Σ

.

This too shall pass

Users Who Are Viewing This Thread (Users: 0, Guests: 3)