Consider the individual graphs of
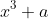
and
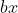
Now there will always be one solution as they cross somewhere in the 3rd quadrant no matter what, however the values of 'a' and 'b' determine how many times they cross in the first quadrant.
As
 = x^3+a)
for
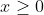
has
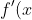 > 0)
, then once this curve reaches a gradient equal to the gradient of
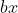
that is a gradient of 'b', then after that there is no possible way for the two curves to intersect. Thus we deal with this condition, and so we find when
 = x^3+a)
has gradient 'b':
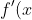 =3x^2)

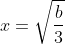
as we are only considering the first quadrant and so
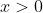
Now if there is only 1 solution, then at
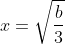
we must see
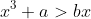
that is:
^3 + a > b\sqrt{\frac{b}{3}})

Similarly, if there are 2 real solutions, then at
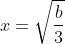
we must see
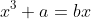
that is:
^3 + a = b\sqrt{\frac{b}{3}})

Lastly, for 3 real solutions, then at
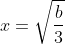
we must see
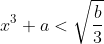
that is:
^3 + a < b\sqrt{\frac{b}{3}})

Now the equation
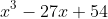
can be re-arranged to
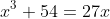
and thus
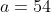
and
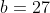
. It follows then that
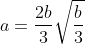
for this equation and there are 2 real solutions.
Now note that this doesn't mean there are 2 real solutions and 1 imaginary solution, it means that there are 2 DISTINCT real solutions, with one of these solutions being a double root.
Hence if we let the roots be

and
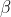
then we can say:
^2(x-\beta) = x^3-27x+54)
Expanding and equating co-efficients gives:
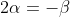
by equating
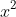
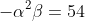
by equating constants.
Thus solving these simultaneously we get:



Now we know that the double root must be in the first quadrant as that is where the two curves
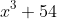
and
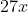
will be tangent to one another. Thus
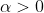
and so we get
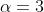
and

Hence
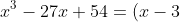^2(x+6))
So the roots are -6 and a double root at 3.
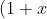^n(1+ \frac{1}{x})^n \equiv \frac{(1+x)^{2n}}{x^n} )


