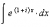HSC 2013 MX2 Marathon (archive) (1 Viewer)

Immortalp00n · Jan 5, 2013

Re: HSC 2013 4U Marathon

RealiseNothing said:
Sorry about that.

okay so sy failed me.
my remaining trust is in you, can i show off my m-deeeek here?

btx3 · Jan 5, 2013

Re: HSC 2013 4U Marathon

Immortalp00n said:
i came to this thread for d babes as per sy's sig
where them bad bitches at?

Sorry man, you were too late. The one available chick in this thread was unfortunately taken by realise just before you, i'll let you know when more babes get here

Immortalp00n · Jan 5, 2013

Re: HSC 2013 4U Marathon

btx3 said:
Sorry man, you were too late. The one available chick in this thread was unfortunately taken by realise just before you, i'll let you know when more babes get here

im disappointed in you lot.
but thanks for the offer <3

asianese · Jan 5, 2013

Re: HSC 2013 4U Marathon

Sy and Realise.. I think the lack of participation comes partly from the range of questions as well as - ITS THE HOLIDAYS! You guys probably forgot that bit

Sy123 · Jan 5, 2013

Re: HSC 2013 4U Marathon

GoldyOrNugget said:
I was playing around with these sorts of problems on the bus the other day, but I ended up confusing myself and didn't get very far.

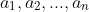
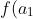Say you had a polynomial with roots $a_1, a_2, ..., a_n$ and you want to find a polynomial with roots $f(a_1), f(a_2), ..., f(a_n)$ (Sy's question would be a special case of this where $f(x) = x + \frac{1}{x}$ ).

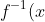You can find an equation with these roots by replacing every instance of $x$ in the polynomial with $f^{-1}(x)$ (this is an interesting property to investigate/prove). In some cases, that equation can be algebraically manipulated into a polynomial without creating any new roots. 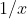This is why the trick of inverting coefficients works for $f(x) = 1/x$ -- it's a shortcut to replacing all $x$ terms with $1/x$ and multiplying out the resulting fractions.

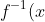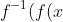When $f(x)$ isn't monotonic (meaning $f^{-1}(x)$ is not a function), it still works; I'm pretty sure you can choose a maximal interval on its domain over which it's monotonic (probably the wrong terminology) and use that for the inverse, because the only necessity is that $f^{-1}(f(x)) = x$ . Also, I'm not convinced that all equations generated in this manner can be manipulated into polynomials without creating new roots (for example, I had some trouble doing it with Sy's question, but I could have just messed up the algebra). Perhaps someone else will have more luck investigating this?

It is relatively simple to prove the first result, and yes it is interesting.
I actually did try this method with my poly question but it didn't seem to output any encouraging results. And yes they probably are not able to be manipulated into polynomial form, but if they aren't in polynomial form - they should be infinitely differentiable right (not rigorous to assume this, but from what I have encountered thus far, they are infinitely differentiable) and hence we can somehow employ Newton's Method of Approximation an infinite number of times right? I have seen a question regarding this.

Proof of the first result:

$P(x)=\sum_{k=0}^{n} c_k x^k$

$$Roots in P$ \ \ \in (\alpha_1,\alpha_2, ... ,\alpha_n)$

Create a function in y, such that the roots are $$Roots in y$ \ \ \in (f(\alpha_1),f(\alpha_2), ... , f(\alpha_n))$

$y=f(\alpha_k) \ \ \alpha_k=f^ {-1}(y)$

$\therefore P(f^ {-1}(y)) = \sum_{k=0}^{1}c_k (f^ {-1}y)^ k$

Which has roots alpha_k for all integers k 0< k <= n

If f is not monotonic increasing/decreasing then we must define the inverse f-1 such in a domain(s) such that this domain stretches over all the roots.

I will explore this further later

seanieg89 · Jan 5, 2013

Re: HSC 2013 4U Marathon

Sy123 said:
It is relatively simple to prove the first result, and yes it is interesting.
I actually did try this method with my poly question but it didn't seem to output any encouraging results. And yes they probably are not able to be manipulated into polynomial form, but if they aren't in polynomial form - they should be infinitely differentiable right (not rigorous to assume this, but from what I have encountered thus far, they are infinitely differentiable) and hence we can somehow employ Newton's Method of Approximation an infinite number of times right? I have seen a question regarding this.

Proof of the first result:

$P(x)=\sum_{k=0}^{n} c_k x^k$

$$Roots in P$ \ \ \in (\alpha_1,\alpha_2, ... ,\alpha_n)$

Create a function in y, such that the roots are $$Roots in y$ \ \ \in (f(\alpha_1),f(\alpha_2), ... , f(\alpha_n))$

$y=f(\alpha_k) \ \ \alpha_k=f^ {-1}(y)$

$\therefore P(f^ {-1}(y)) = \sum_{k=0}^{1}c_k (f^ {-1}y)^ k$

Which has roots alpha_k for all integers k 0< k <= n

If f is not monotonic increasing/decreasing then we must define the inverse f-1 such in a domain(s) such that this domain stretches over all the roots.

I will explore this further later

This method does work for your question although it is not all that fast. I will post this solution and more about this method and it's limitations tomorrow, it was one of my favourite ways of doing such questions.

RivalryofTroll · Jan 5, 2013

Re: HSC 2013 4U Marathon

Also, not really an actual question but I need opinions.

For each of the following topics, which textbook would be better? (I have only SK PATEL Excel MX2 and CAMBRIDGE 4U available)

Categories may include: questions, worked examples, etc.

- Complex Numbers
- Curve Sketching
- Conics
- Polynomials

asianese · Jan 5, 2013

Re: HSC 2013 4U Marathon

RivalryofTroll said:
Also, not really an actual question but I need opinions.

For each of the following topics, which textbook would be better? (I have only SK PATEL Excel MX2 and CAMBRIDGE 4U available)

Categories may include: questions, worked examples, etc.

- Complex Numbers
- Curve Sketching
- Conics
- Polynomials

Get your hands on a Terry Lee for curve sketching and conics...

Sy123 · Jan 5, 2013

Re: HSC 2013 4U Marathon

$$If $ \ \ P(x) \ \ $ and $ \ \ Q(x) \ \ $are polynomials of degrees$ \ \ m \ \ $ and $ \ \ n \ \ $ respectively.$

$$What is the degree of$ \ \ P(Q(x)) \ \ ?$

$The polynomial$ \ \ P(x) \ \ $satisfies the equation$

$P(P(P(x))) - 3P(x) = -2x$

$Show that the degree of$ \ \ P(x) \ \ $ is 1$

$Hence find all polynomials that satisfy this equation$

OMGITzJustin · Jan 5, 2013

Re: HSC 2013 4U Marathon

GoldyOrNugget · Jan 5, 2013

Re: HSC 2013 4U Marathon

Sy123 said:
$$If $ \ \ P(x) \ \ $ and $ \ \ Q(x) \ \ $are polynomials of degrees$ \ \ m \ \ $ and $ \ \ n \ \ $ respectively.$

$$What is the degree of$ \ \ P(Q(x)) \ \ ?$

$The polynomial$ \ \ P(x) \ \ $satisfies the equation$

$P(P(P(x))) - 3P(x) = -2x$

$Show that the degree of$ \ \ P(x) \ \ $ is 1$

$Hence find all polynomials that satisfy this equation$

$$degree of $P(Q(x)) = mn$ \\ \\ If $P(x)$ is of degree $n$ then $P(P(P(x))) - 3P(x)$ is of degree $n^3$, but $P(P(P(x))) - 3P(x) = -2x$ so $n = 1$. \\ \\ Let $P(x) = ax + b$. $P(P(P(x))) - 3P(x) = a(a(ax+b)+b)+b - 3(ax + b) = a(a^2x + ab + b) + b - 3ax - 3b = a^3x + a^2b + ab + b - 3ax - 3b = (a^3 - 3a)x + (a^2b + ab - 2b)$. \\ \\ Equating coefficients, $a^3-3a = -2 \therefore a=1$ or $a=-2$. If $a=1$, $(b + b - 2b) = 0 \therefore b$ can take any value. If $a=-2$, $4b - 2b -2b = 0$ so again b can take any value. \\ So $P(x) = x + b$ or $P(x) = -2x + b$.$

Sy123 · Jan 5, 2013

Re: HSC 2013 4U Marathon

GoldyOrNugget said:
$$degree of $P(Q(x)) = mn$ \\ \\ If $P(x)$ is of degree $n$ then $P(P(P(x))) - 3P(x)$ is of degree $n^3$, but $P(P(P(x))) - 3P(x) = -2x$ so $n = 1$. \\ \\ Let $P(x) = ax + b$. $P(P(P(x))) - 3P(x) = a(a(ax+b)+b)+b - 3(ax + b) = a(a^2x + ab + b) + b - 3ax - 3b = a^3x + a^2b + ab + b - 3ax - 3b = (a^3 - 3a)x + (a^2b + ab - 2b)$. \\ \\ Equating coefficients, $a^3-3a = -2 \therefore a=1$ or $a=-2$. If $a=1$, $(b + b - 2b) = 0 \therefore b$ can take any value. If $a=-2$, $4b - 2b -2b = 0$ so again b can take any value. \\ So $P(x) = x + b$ or $P(x) = -2x + b$.$

Correct - nice work.

GoldyOrNugget · Jan 5, 2013

Re: HSC 2013 4U Marathon

Syyy i'm bored post another question.

P.S. my reasoning for the $x \rightarrow f^{-1}(x)$ roots thing was the same as yours i think. if $(x-a_1)(x-a_2)...(x-a_n) = 0$ is our original polynomial, then we can create one with the new roots as $(x-f(a_1))(x-f(a_2))...(x-f(a_n)) = 0$ since our only requirement is that $x - f(a_i) = 0$ . But if this is the case, then it is also the case that $f^{-1}(x) - a_i = 0$ , which means an equivalent equation is $(f^{-1}(x) - a_1)(f^{-1}(x) - a_2)...(f^{-1}(x) - a_n) = 0$ , and this is exactly the same as our original polynomial except $x \rightarrow f^{-1}(x)$ .

Sy123 · Jan 5, 2013

Re: HSC 2013 4U Marathon

Another one I made - its original:

$Consider the following construction of this particular curve$

Now since I can't draw properly - you must draw it instead, for purposes of this question:

$$The Red variable point$ \ \ = R$

$$Centre of the moving circle$ \ \ = S$

$$Centre of the cartesian plane$ \ \ = O$

$$Radius of large circle is$ \ \ 4a \ \ $radius of small circle is$ \ \ a$ (ignore the scaling on the animation)

$$Denote the point$ \ \ (4a, 0 ) \ \ $as$ \ \ P$

Ok, notation is out of the way, now for the actual question:

=====================================

$i) Show that the parametric equations of the point$ \ \ R \ \ $ is given by$

$x=3a\cos \theta + a\cos \alpha$
$y=3a\sin \theta + a\sin \alpha$

$$Where$ \ \ \alpha = \angle RSO \ \ \ \ \theta = \angle SOP \ \ \ \ \ \ \fbox{3}$

$$ii) You are given that the relationship between$ \ \ \theta \ \ \text{and} \ \ \alpha$
$$is linear, by observing the diagram, find this relationship$ \ \ \ \ \fbox{1}$

$iii) Hence show that the cartesian equation of$ \ \ R \ \ $is given by$

$x^{\frac{2}{3}} + y^ {\frac{2}{3}} = (4a)^{\frac{2}{3}} \ \ \ \ \ \ \fbox{3}$

===============================

If you can't be bothered observing the diagram for part 2, the relationship is:

alpha=-3theta

barbernator · Jan 5, 2013

Re: HSC 2013 4U Marathon

Unsure how difficult/easy this question is.

3 parts:

a) there are 10 rooms in a row. 3 people names allen, bill and chris are placed each in a room by themself. What is the chance that chris is more rooms away from allen than bill.

b) there are n rooms in a row. 3 people names allen, bill and chris are placed each in a room by themself. What is the chance that chris is more rooms away from allen than bill.

c) there are n rooms in a row. m people (m < n) , called a,c,b,d..... What is the chance that the intervals a-b, a-c, a-d, a-e .... are all in increasing distances from each other.

I'll remove and post later if u want sy

Sy123 · Jan 5, 2013

Re: HSC 2013 4U Marathon

barbernator said:
Unsure how difficult/easy this question is.

3 parts:

a) there are 10 rooms in a row. 3 people names allen, bill and chris are placed each in a room by themself. What is the chance that chris is more rooms away from allen than bill.

b) there are n rooms in a row. 3 people names allen, bill and chris are placed each in a room by themself. What is the chance that chris is more rooms away from allen than bill.

c) there are n rooms in a row. m people (m < n) , called a,c,b,d..... What is the chance that the intervals a-b, a-c, a-d, a-e .... are all in increasing distances from each other.

I'll remove and post later if u want sy

no problem lol - if you can notice that the thread is dieing then go right ahead. But I think I'm gonna pass on this question

RealiseNothing · Jan 5, 2013

Re: HSC 2013 4U Marathon

barbernator said:
Unsure how difficult/easy this question is.

3 parts:

a) there are 10 rooms in a row. 3 people names allen, bill and chris are placed each in a room by themself. What is the chance that chris is more rooms away from allen than bill.

b) there are n rooms in a row. 3 people names allen, bill and chris are placed each in a room by themself. What is the chance that chris is more rooms away from allen than bill.

c) there are n rooms in a row. m people (m < n) , called a,c,b,d..... What is the chance that the intervals a-b, a-c, a-d, a-e .... are all in increasing distances from each other.

I'll remove and post later if u want sy

For part (i) I got $\frac{17}{36}$

RealiseNothing · Jan 5, 2013

Re: HSC 2013 4U Marathon

barbernator said:
Unsure how difficult/easy this question is.

3 parts:

a) there are 10 rooms in a row. 3 people names allen, bill and chris are placed each in a room by themself. What is the chance that chris is more rooms away from allen than bill.

b) there are n rooms in a row. 3 people names allen, bill and chris are placed each in a room by themself. What is the chance that chris is more rooms away from allen than bill.

c) there are n rooms in a row. m people (m < n) , called a,c,b,d..... What is the chance that the intervals a-b, a-c, a-d, a-e .... are all in increasing distances from each other.

I'll remove and post later if u want sy

If my part (i) is right then part (ii) is:

$\frac{1}{2}-\frac{n(n-2)}{4!\binom{n}{3}}$

Sy123 · Jan 5, 2013

Re: HSC 2013 4U Marathon

$$i) Show that$ \ \ \ \frac{1+(-1)^{n+1}x^{2n}}{1+x^2} = 1-x^2+x^4-x^6+...+(-1)^ {n-1} x^ {2n-2} \ \ \ \ \ \fbox{0}$

$ii) By creating an inequality of lower bounds and upper bounds, then taking n to infinity. Prove that$

$\tan^{-1}x = x- \frac{x^3}{3}+\frac{x^5}{5}- \frac{x^7}{7}+... \equiv \sum_{n=0}^{\infty} \frac{(-1)^{n} x^{2n+1}}{(2n+1)} \ \ \ \ \ \fbox{4}$

Carrotsticks · Jan 5, 2013

Re: HSC 2013 4U Marathon

Sy123 said:
I finally found a way to find the taylor series of tan-1 x without the non-rigour:

$$i) Show that$ \ \ \ \frac{1+(-1)^{n+1}x^{2n}}{1+x^2} = 1-x^2+x^4-x^6+...+(-1)^ {n-1} x^ {2n-2} \ \ \ \ \ \fbox{0}$

$ii) By creating an inequality of lower bounds and upper bounds, then taking n to infinity. Prove that$

$\tan^{-1}x = x- \frac{x^3}{3}+\frac{x^5}{5}- \frac{x^7}{7}+... \equiv \sum_{n=0}^{\infty} \frac{(-1)^{n} x^{2n+1}}{(2n+1)} \ \ \ \ \ \fbox{4}$

There's a bit more to it than that =p

Firstly, we must have x lying on the unit circle as that is the maximal radius for which convergence occurs.

Secondly, you should probably add a part where they evaluate the integral of the n+1'th term, generally called the Error Term E(x), which you will then need to prove converges to 0 as n gets large.

Thirdly, it would be in your best interest to use say t as a dummy variable, and then integrate from 0 to x, where |x|<1, so then you can avoid issues with the constant term etc.

HSC 2013 MX2 Marathon (archive) (1 Viewer)

Member

Active Member

Member

Σ

This too shall pass

Well-Known Member

Sleep Deprived Entity

Σ

This too shall pass

Well-Known Member

Señor Member

This too shall pass

Señor Member

This too shall pass

Active Member

This too shall pass

what is that?It is Cowpea

what is that?It is Cowpea

This too shall pass

Retired

Users Who Are Viewing This Thread (Users: 0, Guests: 1)