Re: HSC 2013 4U Marathon
Here is my solution to the question.
==============
Ok, so we need to model the moving marker, and I know I can simplify the problem by finding the parametric equations of the red marker.
So I need to find the parametric equations of the marker, but since this red marker is dependent on the circle. I will first investigate the circle to see what I can find:
Establish the equation of the circle:
^2+(y-1)^2 = 1 )
For some variable centre (p,1).
Now I know that the parametric equations of this circle is:


These equations are able to give me any point I want on that circle, and the point we want to model or represent is the red marker.
So we need to find a relationship between p and theta such that they model the red marker.
This is why the time variable is useful to imagine the following situation. Ok, so our circle makes 1 revolution per second, but its rolling, hence the distance the centre covers in 1 second, is equal to the circumference (draw this out if it doesn't make sense)
Hence,
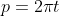
Now we need to find a way to model theta in terms of t. This is easy enough anyway, every second theta increases by 2pi, hence

However we need to be careful here, theta is actually decreasing, as in it is increasing in the negative direction since our theta is going clockwise (as stated in the question), hence indeed it comes about that:

Recall the initial condition for the red marker being (0,0) When the circle has an equation of
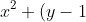^2 = 1 )
However when theta is zero initially, our inital conditions become (1,1). To make our inital conditions (0,0) we must take away pi/2 to theta (imagine the unit circle of trigonometry, similar logic is involved).
Hence our new equations are:
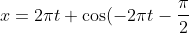 )
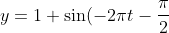 )
Simplification
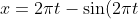 )
)
Now we have the parametric equations, we now need to isolate one and form the cartesian equation:
 )
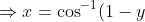 - \sin (\cos^{-1}(1-y)) )
Use the right angle triangle in order to simplify the second term
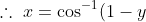 - \sqrt{y(2-y)} )


