Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
WLWLWLWLWLWLWLWLWLWLWLWLWLWLWLWLWLWLWL WWWWW WWWWW and then win.
And this can go on infinitely many times, so infinite series are involved. I was experimenting with $2, whether he wins up to 4.
When he has $2, (also I made probability p so its easier), I seperated each decision into two groups, so each game he plays will have a structure like:
(WL) , (WL) , (LW) , (WL) , .... (WL) , (WW).
It doesn't matter what order the L and W's are after each partition, so the probability is
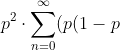)^n = \frac{p^2}{p^2-p+1} )
So yeah this might help some other people in trying to find the answer to the problem.
But for example, if we denote W as win, and L as Loss, he can go:Yeah that makes more sense.
So then would it be......
a)
P($20) = 10C0 (18/37)^10(19/37) + 10C1(18/37)^11(19/37) + 10C2(18/37)^12(19/37)^2 + 10C3(18/37)^13(19/37)^3 +10C4(18/37)^14(19/37)^4 + 10C5(18/37)^15(19/37)^5 + 10C6(18/37)^16(19/37)^6 +10C7(18/37)^17(19/37)^7 + 10C8(18/37)^18(19/37)^8 + 10C9(18/37)^19(19/37)^9
P($0) = 1- P($20)
b) If he makes a single bet with his money, he will have a higher probability of winning.
However, he has a higher probability of losing as well.
If he only wants to make a few dollars, it is better for him to bet $1 at a time.
If he only wants double-or-nothing then he must do it all in one bet.
?????? For some reason I am thinking that I missed something again.
WLWLWLWLWLWLWLWLWLWLWLWLWLWLWLWLWLWLWL WWWWW WWWWW and then win.
And this can go on infinitely many times, so infinite series are involved. I was experimenting with $2, whether he wins up to 4.
When he has $2, (also I made probability p so its easier), I seperated each decision into two groups, so each game he plays will have a structure like:
(WL) , (WL) , (LW) , (WL) , .... (WL) , (WW).
It doesn't matter what order the L and W's are after each partition, so the probability is
So yeah this might help some other people in trying to find the answer to the problem.
Last edited:

