Re: HSC 2013 4U Marathon
Am disappointed that no-one has answered Sy's conjugate root question!
Can you please criticise this proof? I am starting to have doubts about it.
===
Start with the polynomial,

We need to make the lowest reducible rational polynomial that has that as a root, so we simply:
^2 - q = 0 )
The above polynomial has the root
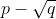
It is the simplest most reducible rational polynomial that has p + root(q) as a root.
Now consider:
 = a_1(x) a_2(x) \dots a_n(x) )
Where a_1, a_2 ... are all rational polynomial functions of lowest reducibility.
If
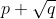
is a root then among the series a_1, a_2... there must exist a_k for some k such that
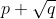
is a root.
Since a_k is irreducible and rational, then that polynomial must be:
 = (x-p)^2 - q )
And that polynomial also has the root

Therefore that is also a root of P(x).
Is there a gap or something in this? Or is it all good?
^{n+1}})

