Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
HSC 2013 MX2 Marathon (archive) (1 Viewer)
- Thread starter Sy123
- Start date
- Status
- Not open for further replies.
RealiseNothing
what is that?It is Cowpea
Re: HSC 2013 4U Marathon
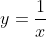 from the x-values n to n+k. Construct an upper bound rectangle from n to n+k as the width, and f(n) as the height. This will give the inequality:
from the x-values n to n+k. Construct an upper bound rectangle from n to n+k as the width, and f(n) as the height. This will give the inequality:
-(n)]f(n))
-\ln(n) < \frac{k}{n})
 < \frac{k}{n})
 < \frac{k}{n})
 < k)
^n] < k)
^n < e^k)
Then do something similar for the lower bound, but I am still doing that so will edit it in.
Consider the curve
Then do something similar for the lower bound, but I am still doing that so will edit it in.
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,467
- Gender
- Undisclosed
- HSC
- N/A
Re: HSC 2013 4U Marathon
Also Sy, how did you expect students to prove the existence of it without the monotone convergence theorem?
In my paper, students were given the existence of the E-M constant. Sy's question is proving its existence.Very similar to last year's BOS trial question 15 by carrot.
Also Sy, how did you expect students to prove the existence of it without the monotone convergence theorem?
Last edited:
RealiseNothing
what is that?It is Cowpea
Re: HSC 2013 4U Marathon
By considering an isosceles triangle with one of it's angles 108 degrees, prove that:
 = \frac{1}{1+\sqrt{5}})
By considering an isosceles triangle with one of it's angles 108 degrees, prove that:
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
The limit should be able to be done simply using squeeze theorem

From the sine rule of a triangle:
}{\sin \theta} = \frac{B}{A} )

Now, using the cosine rule on angle theta:

Now on the larger angel:
 = \frac{2A^2-B^2}{2A^2} = 4\cos^3 \theta - 3\cos \theta = \cos \theta(4\cos^2 \theta - 1- 2) )
Now:
 )
Simplifying:

^2 - \frac{B}{A} - 1= 0 )

Now, we know that:
 = \sqrt{\frac{1}{2} \left( 1 - \frac{B}{2A} \right)} = \frac{1}{2} \sqrt{2-\frac{B}{A}} )
Substituting in the value for B/A we get:
 = \frac{1}{2} \sqrt{\frac{3-\sqrt{5}}{2}} = \frac{1}{2} \sqrt{\frac{(1-\sqrt{5})^2}{4}} = \frac{|1-\sqrt{5}|}{4} = \frac{1}{1+\sqrt{5}} )
I feel like I took a long approach
I expected students to do something similar to what Realise did. Does the existence of the limit need to be specified despite the upper bound that is independent of n?In my paper, students were given the existence of the E-M constant. Sy's question is proving its existence.
Also Sy, how did you expect students to prove the existence of it without the monotone convergence theorem?
The limit should be able to be done simply using squeeze theorem
Let the equal sides of the triangle be A and the side opposite 108 degrees be B.By considering an isosceles triangle with one of it's angles 108 degrees, prove that:
 = \frac{1}{1+\sqrt{5}})
From the sine rule of a triangle:
Now, using the cosine rule on angle theta:
Now on the larger angel:
Now:
Simplifying:
Now, we know that:
Substituting in the value for B/A we get:
I feel like I took a long approach
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,467
- Gender
- Undisclosed
- HSC
- N/A
Re: HSC 2013 4U Marathon
2. Squeeze Theorem is usually used to find the closed form for some sort of sequence/series/limit. Gamma, as we know so far, has no single closed form.
1. Don't quite get what you mean by the upper bound of gamma being independent of n.I expected students to do something similar to what Realise did. Does the existence of the limit need to be specified despite the upper bound that is independent of n?
The limit should be able to be done simply using squeeze theorem
2. Squeeze Theorem is usually used to find the closed form for some sort of sequence/series/limit. Gamma, as we know so far, has no single closed form.
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
For that one, I aimed for students to first consider the upper rectangles of the graph y=1/x from x=1 to x=(n)

 > 0 )
 > 0 )
Now the lower rectangles from x=2 to x=n
 < \int_0^{n} \frac{dx}{x} )


So no matter how n increases, it will always be less than 1, and greater than zero, thus converging to a finite limit.
Is this incorrect?
Ah sorry I thought you meant the e^k question for some reason.1. Don't quite get what you mean by the upper bound of gamma being independent of n.
2. Squeeze Theorem is usually used to find the closed form for some sort of sequence/series/limit. Gamma, as we know so far, has no single closed form.
For that one, I aimed for students to first consider the upper rectangles of the graph y=1/x from x=1 to x=(n)
Now the lower rectangles from x=2 to x=n
So no matter how n increases, it will always be less than 1, and greater than zero, thus converging to a finite limit.
Is this incorrect?
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,467
- Gender
- Undisclosed
- HSC
- N/A
Re: HSC 2013 4U Marathon
Yep, that is incorrect. A counter-example would be the curve y=sin(x). It is always less than 1 and greater than -1, but it most certainly does NOT converge to a finite limit.Ah sorry I thought you meant the e^k question for some reason.
For that one, I aimed for students to first consider the upper rectangles of the graph y=1/x from x=1 to x=(n)
Now the lower rectangles from x=2 to x=n
So no matter how n increases, it will always be less than 1, and greater than zero, thus converging to a finite limit.
Is this incorrect?
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
Apologies
EDIT: What if I showed
 >H_{n+1} - \ln(n+1) )
And then made the argument that as n increases H_n - ln(n) keeps decreasing however it is bounded on the lower by 0, then it approaches some finite limit?
We can show the above by simply showing that, then subbing in x=1/n
 > \frac{x}{x+1} )
Which can be done through calculus.
Ah yep that is trueYep, that is incorrect. A trivial example is to consider the curve y=sin(x). It is always less than 1 and greater than -1, but it most certainly does NOT converge to a finite limit.
Apologies
EDIT: What if I showed
And then made the argument that as n increases H_n - ln(n) keeps decreasing however it is bounded on the lower by 0, then it approaches some finite limit?
We can show the above by simply showing that, then subbing in x=1/n
Which can be done through calculus.
Last edited:
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,467
- Gender
- Undisclosed
- HSC
- N/A
Re: HSC 2013 4U Marathon
No need for apologies, this is how we learn things =) By making mistakes.
No need for apologies, this is how we learn things =) By making mistakes.
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,467
- Gender
- Undisclosed
- HSC
- N/A
Re: HSC 2013 4U Marathon
That is the monotone convergence theorem, as I mentioned earlier =)Ah yep that is true
Apologies
EDIT: What if I showed
And then made the argument that as n increases H_n - ln(n) keeps decreasing however it is bounded on the lower by 0, then it approaches some finite limit?
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
Ah ok thanks for the clarificationThat is the monotone convergence theorem, as I mentioned earlier =)
RealiseNothing
what is that?It is Cowpea
Re: HSC 2013 4U Marathon

Now one of the smaller triangles has angles 36, 36, 108, and thus is similar to the larger triangle. We can also easily find the side lengths of the smaller triangle and use the ratio of the matching sides of the similar triangles to obtain:

Solving for gives:
gives:



Now we use the sine rule on the larger triangle to obtain:
}{1} = \frac{\sin(108)}{x})
Now = 2\sin(18)\cos(18)) and
and  = \sin(72) = \cos(18))
Substituting these in to what we have gives:
\cos(18) = \frac{\cos(18)}{x})
Cancelling out the) and dividing both sides by 2 gives:
and dividing both sides by 2 gives:
 = \frac{1}{2x})
Substituting in our value for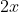 gives the result:
gives the result:
 = \frac{1}{1+\sqrt{5}})
My approach was to split the triangle into two smaller triangles by dividing the 108 angle into 72 and 36 angles and connecting that vertex to the opposite side. Let the equal sides of the larger triangle be 1, and the side opposite the 108 angle be someI expected students to do something similar to what Realise did. Does the existence of the limit need to be specified despite the upper bound that is independent of n?
The limit should be able to be done simply using squeeze theorem
Let the equal sides of the triangle be A and the side opposite 108 degrees be B.
From the sine rule of a triangle:
Now, using the cosine rule on angle theta:
Now on the larger angel:
Now:
Simplifying:
Now, we know that:
Substituting in the value for B/A we get:
I feel like I took a long approach
Now one of the smaller triangles has angles 36, 36, 108, and thus is similar to the larger triangle. We can also easily find the side lengths of the smaller triangle and use the ratio of the matching sides of the similar triangles to obtain:
Solving for
Now we use the sine rule on the larger triangle to obtain:
Now
Substituting these in to what we have gives:
Cancelling out the
Substituting in our value for
RealiseNothing
what is that?It is Cowpea
Re: HSC 2013 4U Marathon
In the spirit of the AMC coming up next Thursday, here is a nice question from last year's paper:

In the spirit of the AMC coming up next Thursday, here is a nice question from last year's paper:
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
My Solution
I got 840 and I think i got a more logical answer now:In the spirit of the AMC coming up next Thursday, here is a nice question from last year's paper:

My Solution
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
It is clear through Demoivre's theorem:
 + \cos(3x) + \dots + \cos (nx) = \frac{\sin \left(n+\frac{1}{2})x}{\sin\frac{x}{2}} - \frac{1}{2} )
Substituting in
We get:
 = 0 \ \ $iff$ \ \frac{m}{d} \ $is not an integer$ )
Taking the case of m/d being an integer, we look at the series version of f(m,d) it is clear that:
 = 1 \ \ $iff$ \ \frac{m}{d} \ $is an integer$ )
There is no other case.
2.
I'm going to guess that
g(n) = f(x(n), y(n))
}{y(n)} = $integer$ \ \ $for prime$ \ n )
And not an integer for composite n.
Now,from your earlier paper about the formula for primes lie, the property of prime numbers:
! \equiv -1 \mod{p} )
I still don't know how to prove this but I'm going to take it as true
Thus, we can see that
 = (n-1)!+1 )
 = n )
Therefore:
 = f((n-1)! + 1, n) )
3.
 = n \cdot g(n) )
===
Hopefully that is correct
1.
It is clear through Demoivre's theorem:
Substituting in
We get:
Taking the case of m/d being an integer, we look at the series version of f(m,d) it is clear that:
There is no other case.
2.
I'm going to guess that
g(n) = f(x(n), y(n))
And not an integer for composite n.
Now,from your earlier paper about the formula for primes lie, the property of prime numbers:
I still don't know how to prove this but I'm going to take it as true
Thus, we can see that
Therefore:
3.
===
Hopefully that is correct
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
Re: HSC 2013 4U Marathon
Your answer is quite close, but your p(n) will actually spit out (1,2,3,0,5,0,7,0,0,0,11,etc) rather than (2,3,5,7,etc).
Well you don't need to know how to prove the factorial thing, think about the definition of a prime number...it is convenient that we have found a function f that "checks divisibility".1.
It is clear through Demoivre's theorem:
Substituting in
We get:
Taking the case of m/d being an integer, we look at the series version of f(m,d) it is clear that:
There is no other case.
2.
I'm going to guess that
g(n) = f(x(n), y(n))
And not an integer for composite n.
Now,from your earlier paper about the formula for primes lie, the property of prime numbers:
I still don't know how to prove this but I'm going to take it as true
Thus, we can see that
Therefore:
3.
===
Hopefully that is correct
Your answer is quite close, but your p(n) will actually spit out (1,2,3,0,5,0,7,0,0,0,11,etc) rather than (2,3,5,7,etc).
- Status
- Not open for further replies.


