Re: HSC 2013 4U Marathon
let dv=xdx
Use IBP
let u = logx then use base conversionintegral of xlogx
let dv=xdx
Use IBP
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
let u = logx then use base conversionintegral of xlogx
Why would you need to base convert? It is understood that logx means log to the base e of ex = lnx.let u = logx then use base conversion
let dv=xdx
Use IBP
The polynomial with roots:
The polynomial with roots:
So we have a polynomial with roots +alpha and a polynomial with roots -alpha
So how to make a polynomial that is a combination of these roots, we have to multiply them, we can observe this by simply writing each polynomial as (x-a_1)(x-a_2)...(x-a_2n)
Then if we multiply them and we get a polynomial with both roots!
So the polynomial T(y) has roots
=S(y) \cdot S(-y) )
I see what you did there.....The polynomial with roots:
So we have a polynomial with roots +alpha and a polynomial with roots -alpha
So how to make a polynomial that is a combination of these roots, we have to multiply them, we can observe this by simply writing each polynomial as (x-a_1)(x-a_2)...(x-a_2n)
Then if we multiply them and we get a polynomial with both roots!
So the polynomial T(y) has roots
=[B][U]S(y) \cdot S(-y)[/U][/B] )
x = arccost ..[1]
I made a mistake in my solution (by interchanging doing something with (sin^-1, cos^-1) in the middle of it hence muddling my solution up), it is indeed supposed to be:x = arccost ..[1]
y = arcsint ..[2]
[1] + [2]
x + y = pi/2
y = pi/2 - x
x = arccost, with 0 < x < pi (x=pi)
THerefore 0 < x < \pi/2 , |x| = |arccost|
y= pi/2 -|x|
Pretty sure its wrong but worth a stab:Let
Find a recurrence formula for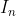
That's a very standard induction question that appears in 4U a lot. If only the subscripts were non-ambiguous though.....A good induction problem for the ones out there close to my level
The sequence of numbers x0, x1, x2, . . . begins with x0 = 1 and x1 = 1 and is then recursively determined by the
equations
xn+2 = 4xn+1 − 3xn + 3
n
for n ≥ 0.
(a) Find the values of x2, x3, x4 and x5.
(b) Can you find a solution of the form
xn = A + B × 3
n
+ C × n3
n
which agrees with the values of x0, . . . , x5 that you have found?
(c) Use induction to prove that this is the correct formula for xn for all n ≥ 0.
Here's the link, sorry bout the copy horse person.If only the subscripts were non-ambiguous though.....
Interesting question:Here's the link, sorry bout the copy horse person.
http://www.maths.ox.ac.uk/files/imp...graduate/practice-problems/pdf/induction2.pdf

