RealiseNothing
what is that?It is Cowpea
Re: HSC 2014 4U Marathon - Advanced Level
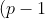! = (p-1)(a_0p+1)(a_1p+1)(a_2p+1)...(a_kp+1))
Which becomes a polynomial of the form:
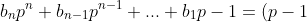!)
Take the constant term to the other side and we are done. Note were just arbitrarily chosen to represent whatever value it's meant to be as it really doesn't matter the amount of terms present.
were just arbitrarily chosen to represent whatever value it's meant to be as it really doesn't matter the amount of terms present.
The only thing you would really have to prove is the first line where we factorised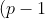!) is only legit for primes. Though this is easily done by considering that if
is only legit for primes. Though this is easily done by considering that if  is an integer such that
is an integer such that  then
then  is a multiple of
is a multiple of 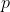 IFF
IFF 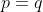 . Then it is forced that all preceding integers of
. Then it is forced that all preceding integers of 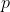 must be a remainder of
must be a remainder of  for
for  otherwise you end up stuck in a pattern of remainders that will never be 0 (hence contradiction).
otherwise you end up stuck in a pattern of remainders that will never be 0 (hence contradiction).
So there exist some such that
such that  and the uniqueness of this is trivial.
and the uniqueness of this is trivial.
Yer my approach was showing that:For the probability question I got 3361/6561.
I just enumerated the colourings that don't contain a non-degenerate red triangle as follows:
(Colourings with less than 3 red points) + (Colourings with 3 red collinear points).
For Wilson's theorem, you could show that:
(~) If p is prime, then every nonzero a in {0,1,2,...,p-1} has a multiplicative inverse b (mod p), and that 1 and (p-1) are the only numbers that are self-inverse.
Once you have (~), the product (p-1)! cancels out in pairs except for the first and last term. This leaves a residue of 1*(p-1)=-1 mod p. This proves one direction of Wilson's and the converse is trivial.
To make this an extension two solution, I think we could just recast (~) as
For any prime p and any positive integer a there is a positive integer b such that ab-1 is divisible by p. Moreover, if b' is another such integer, then b-b' must be divisible by p. Also, if a-b is divisible by p and ab-1 is divisible by p, then either a-1 or a+1 is divisible by p.
Knowing about division/remainders is in the course, so this modified statement leads to a proof without mentioning anything out of syllabus I think.
Which becomes a polynomial of the form:
Take the constant term to the other side and we are done. Note
The only thing you would really have to prove is the first line where we factorised
So there exist some


