leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,768
- Gender
- Male
- HSC
- 2015
I do not feel at home without this...
------------------------------------------------------------
Here post integrals for helping 2016 students with integration!
Do not post a question until the last one is answered
(Reference to Sy123 for the copy and paste)
------------------------------------------------------------
FIRST QUESTION:
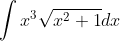
------------------------------------------------------------
Here post integrals for helping 2016 students with integration!
Do not post a question until the last one is answered
(Reference to Sy123 for the copy and paste)
------------------------------------------------------------
FIRST QUESTION:

