davidgoes4wce
Well-Known Member
Re: HSC 2017 MX2 Marathon
Not sure if its me or the book error but I had a complex number question
(6+i)(a+bi)=2
My solution for
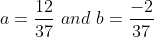
My book has a different solution to that.
Not sure if its me or the book error but I had a complex number question
(6+i)(a+bi)=2
My solution for
My book has a different solution to that.