-
Looking for HSC notes and resources? Check out our Notes & Resources page
MX2 Marathon (1 Viewer)
- Thread starter dan964
- Start date
For the chord in a circle problem, see also https://en.wikipedia.org/wiki/Bertrand_paradox_(probability).
What course you planning on doing (if you want to say)?@blyatman once i was REALLy into programming and was doing programming comp qtns for fun. And I also remember writing code for the probability of getting a chord less than a diameter in a unit circle too. GOod old days
blyatman
Well-Known Member
- Joined
- Oct 11, 2018
- Messages
- 539
- Gender
- Undisclosed
- HSC
- N/A
That was an interesting read, never thought about it that way.For the chord in a circle problem, see also https://en.wikipedia.org/wiki/Bertrand_paradox_(probability).
stupid_girl
Active Member
- Joined
- Dec 6, 2009
- Messages
- 221
- Gender
- Undisclosed
- HSC
- N/A
Shall we have geometry again? It would be interesting if geometry can be given more weight in its final MX2 year.
AB is a chord of a circle with centre O. Extend AB to C and extend OB to D such that AC=OC, AD||OC and ∠ACD=15°. Find BC:BD.
AB is a chord of a circle with centre O. Extend AB to C and extend OB to D such that AC=OC, AD||OC and ∠ACD=15°. Find BC:BD.
TheOnePheeph
Active Member
- Joined
- Dec 13, 2018
- Messages
- 241
- Gender
- Male
- HSC
- 2019
I sure hope that geometry doesn't have more of a weight in this exam, convoluted geo questions are the absolute worst.Shall we have geometry again? It would be interesting if geometry can be given more weight in its final MX2 year.
AB is a chord of a circle with centre O. Extend AB to C and extend OB to D such that AC=OC, AD||OC and ∠ACD=15°. Find BC:BD.
Is the answer to that problem
stupid_girl
Active Member
- Joined
- Dec 6, 2009
- Messages
- 221
- Gender
- Undisclosed
- HSC
- N/A
YesIs the answer to that problemthough?
stupid_girl
Active Member
- Joined
- Dec 6, 2009
- Messages
- 221
- Gender
- Undisclosed
- HSC
- N/A
HeroWise
Active Member
- Joined
- Dec 8, 2017
- Messages
- 353
- Gender
- Male
- HSC
- 2020
TheOnePheeph can u work out the previous one if possible
TheOnePheeph
Active Member
- Joined
- Dec 13, 2018
- Messages
- 241
- Gender
- Male
- HSC
- 2019
Wait the one just posted or the one before that which I said wasTheOnePheeph can u work out the previous one if possible
TheOnePheeph
Active Member
- Joined
- Dec 13, 2018
- Messages
- 241
- Gender
- Male
- HSC
- 2019
Here you go, just wrote it up now. Know that there is likely an easier way of doing this, but my solution is the first way I saw, and does yield the correct answer.The latter. Take your time man
Attachments
-
835.5 KB Views: 14
-
646 KB Views: 9
HeroWise
Active Member
- Joined
- Dec 8, 2017
- Messages
- 353
- Gender
- Male
- HSC
- 2020
OK so my way was not way off. Mine went off in tangents b4 i came to the required result. @stupid_girl is there a faster way?
stupid_girl
Active Member
- Joined
- Dec 6, 2009
- Messages
- 221
- Gender
- Undisclosed
- HSC
- N/A
A solution based on elementary geometry will just be more convoluted.OK so my way was not way off. Mine went off in tangents b4 i came to the required result. @stupid_girl is there a faster way?
If you have attempted the hardest easy geometry problem (google it if you haven't), then you should see that sine rule can save you from constructing many additional lines.
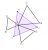
We constructgeometry again
In the figure, ABC, ADE and AFG are equilateral triangles. H, I and J are the mid-points of CD, EF and GB respectively. Find HI:IJ.
View attachment 27263
Finally, if we let
Last edited:
stupid_girl
Active Member
- Joined
- Dec 6, 2009
- Messages
- 221
- Gender
- Undisclosed
- HSC
- N/A
Was this one solved?
^2=\left(-1\right)^n$.)
If you like to play with induction, you may also try
^{2n+1}-a^{2n+1}-b^{2n+1}$ is divisible by $ab(a+b)$.)
Having said that, it is in fact easier to do it without induction.
If you like to play with induction, you may also try
Having said that, it is in fact easier to do it without induction.
blyatman
Well-Known Member
- Joined
- Oct 11, 2018
- Messages
- 539
- Gender
- Undisclosed
- HSC
- N/A
Can anyone help me on this one?
Consider the Riemann zeta function , defined as
, defined as
=\sum_{n=1}^\infty\frac{1}{n^s})
where is complex with a real part greater than 1.
is complex with a real part greater than 1.
Prove that the real part of every non-trivial zero of the Riemann zeta function is .
.
If you work it out, please don't post it here but DM me.
I'll pay you $10, and I'm already taking a risk here. Also, after you send it to me, you must destroy your copy (this part is VERY IMPORTANT and non-negotiable).
Consider the Riemann zeta function
where
Prove that the real part of every non-trivial zero of the Riemann zeta function is
If you work it out, please don't post it here but DM me.
I'll pay you $10, and I'm already taking a risk here. Also, after you send it to me, you must destroy your copy (this part is VERY IMPORTANT and non-negotiable).
No, DM me - I'll pay $100 for it!Can anyone help me on this one?
Consider the Riemann zeta function, defined as
whereis complex with a real part greater than 1.
Prove that the real part of every non-trivial zero of the Riemann zeta function is.
If you work it out, please don't post it here but DM me.
I'll pay you $10, and I'm already taking a risk here. Also, after you send it to me, you must destroy your copy (this part is VERY IMPORTANT and non-negotiable).
I'll pay $1000, how about thatCan anyone help me on this one?
Consider the Riemann zeta function, defined as
whereis complex with a real part greater than 1.
Prove that the real part of every non-trivial zero of the Riemann zeta function is.
If you work it out, please don't post it here but DM me.
I'll pay you $10, and I'm already taking a risk here. Also, after you send it to me, you must destroy your copy (this part is VERY IMPORTANT and non-negotiable).
First q: Note thatWas this one solved?
If you like to play with induction, you may also try
Having said that, it is in fact easier to do it without induction.
and then check base cases to get the result.
Second q: Note that
where we note the fractions are integers as