Re: International Baccalaureate Maths Marathon
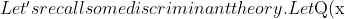 = ax^{2} + bx + c$ be a real quadratic (i.e. the coefficients $a,b,c$ are real numbers) and $a \neq 0$. Let $\Delta = b^{2} - 4ac$ be the discriminant. Then we have$)
 \text{ has two distinct real roots } \iff Q(x) \text{ is strictly positive in some places and strictly negative in other places}$$)
 \text{ has a double real root } \iff Q(x) \text{ is either always non-negative or non-positive (depending on the sign of }a) \text{ and attains the value 0 at some real }x$$)
 \text{ has no real root } \iff Q(x) \text{ is either always (strictly) negative or positive (depending on the sign of }a).$$)
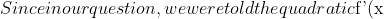$ was non-negative always, one of the last two bullet points above applies, so we have either $\Delta = 0$ or $\Delta < 0$, i.e. we have $\Delta \leq 0$.$)
And sorry I typoed before, I wrote non-negative for the discriminant but meant to say non-positive. I have corrected this now.
I'll take your word for it Integrand, I am still confused as to what non-negative means in this case.
I thought the discriminant for sure wasreading the question first up.
And sorry I typoed before, I wrote non-negative for the discriminant but meant to say non-positive. I have corrected this now.


