alussovsky
Member
- Joined
- May 17, 2018
- Messages
- 39
- Gender
- Male
- HSC
- 2019
So I came across this induction question and am quite stuck mid-way.
The question is: Prove that is divisible by
is divisible by  for all odd integers
for all odd integers 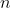
So far, I have this working out done:
1. To prove: , where
, where 
Prove true for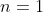
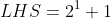
 which is divisible by 3
which is divisible by 3
So the statement is true for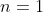
2. Assume true for , where
, where 
i.e. , where
, where 
3. Prove true for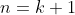
To prove: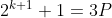 , where
, where 
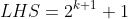
Aaaand I'm stuck at that step. I've no idea how to manipulate the LHS so that the assumption from 2 can be subbed into 3. Also, is the working so far correct? Thanks!
The question is: Prove that
So far, I have this working out done:
1. To prove:
Prove true for
So the statement is true for
2. Assume true for
i.e.
3. Prove true for
To prove:
Aaaand I'm stuck at that step. I've no idea how to manipulate the LHS so that the assumption from 2 can be subbed into 3. Also, is the working so far correct? Thanks!
