Hi guys,
I have a couple of questions that I need help with:
1. Find d/dx ∫8~x (2t^5 - 3)^6 dt.
Answer: (2x^5-3)^6
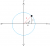
2. Find ∫3√2~6 √(36-x^2) dx by using the formula for area of a segment.
Answer: 9(π/2-1)
Note: ∫a number ~ another number are the limits of the integration.
Thanks
I have a couple of questions that I need help with:
1. Find d/dx ∫8~x (2t^5 - 3)^6 dt.
Answer: (2x^5-3)^6
2. Find ∫3√2~6 √(36-x^2) dx by using the formula for area of a segment.
Answer: 9(π/2-1)
Note: ∫a number ~ another number are the limits of the integration.
Thanks