One definition of an ellipse that is mathematically equivalent to the focus-directrix definition is:
An ellipse is the locus of points

that are related to two distinct fixed points
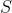
and
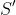
(its foci) by the relationship
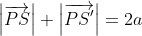
where
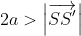
from which it follows that:
- the centre of the ellipse is at the midpoint of
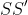
- the fixed points
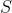 and
and 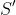 lie on the major axis, which has length
lie on the major axis, which has length 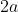 between the intercepts
between the intercepts
- the ellipse is symmetrical (ie. each has is a mirror image) in the major and minor axis, the minor axis being perpendicular to the major axis and through the centre.
Note that:
- The requirement that
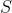 and
and 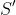 be distinct is because when they coincide, the locus becomes a circle.
be distinct is because when they coincide, the locus becomes a circle.
- If
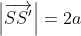 then the locus is a single point, the midpoint of
then the locus is a single point, the midpoint of 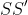 .
.
- If
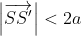 then there is no locus.
then there is no locus.
Using vectors, these facts should be sufficient to solve the rest of the problem.
Consequently, a question like this could be asked as an example of the overlap between the complex numbers and vectors topics, so long as sufficient support material was provided.