I think he is referring case of k = -2 which I missed.
To shift a graph k units to the left the transformation is f(x+k) where k is positive.
Yes, I am.
And
@Dashdorm24, you can check each is valid by doing the transformation and seeing that the resulting
)
has

as a factor.
For example, taking
 = (x + 1)(x - 2)^2)
(which is the same as
 = (u + 1)(u - 2)^2)
, I'm just using
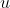
as a dummy variable so that the transformation is clearer), and performing the transformation
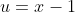
, as suggested by
@cossine, gives:
 &= (u + 1)(u - 2)^2 \\ P(x - 1) &= \big[(x - 1) + 1\big]\big[(x - 1) - 2\big]^2 \quad \quad \text{putting $u = x - 1$} \\ &= x(x - 3)^2 \\ \text{So} \quad y &= x(x -3)^2 \quad \text{is the transformed polynomial} \end{align*})
and it has a single root at the origin and a double root at
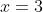
, just as would be expected from a shift of one unit to the right.
The second transformation,
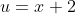
, which
@cossine correctly identified from my hint, should produce a shift of 2 units to the left, moving the double root to the origin. Checking:
 &= (u + 1)(u - 2)^2 \\ P(x + 2) &= \big[(x + 2) + 1\big)\big[(x + 2) - 2\big]^2 \quad \quad \text{putting $u = x + 1$} \\ &= (x + 3)x^2 \\ \text{So} \quad y &= x^2(x +3) \quad \text{is the transformed polynomial} \end{align*})
and it has a single root at
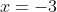
and a double root at the origin, just as would be expected from a shift of two units to the left.
Noting that our given polynomial
 = (x + 1)(x - 2)^2)
has
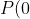 = 4)
, we can also predict that a shift downwards by 4 should give a transformed polynomial with a root at the origin. Check:
 &= (x + 1)(x - 2)^2 \\ P(x) + 4 &= (x + 1)(x - 2)^2 \quad \quad \text{putting $P(x) = Q(x) - 4$} \\ P(x) &= (x + 1)(x - 2)^2 - 4 \\ &= (x + 1)\left(x^2 - 4x + 4\right) - 4 \\ &= x^3 - 4x^2 + 4x + x^2 - 4x + 4 - 4 \\ &= x^3 - 3x^2 \\ \text{So} \quad P(x) &= x^2(x - 3) \quad \text{is the transformed polynomial} \end{align*})
and it has a single root at
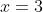
and a double root at the origin, just as would be expected from a shift of four units to the down. (The point
)
lies on the original polynomial, so a shift down of four should produce a root of the new polynomial at
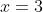
.)
These techniques can be combined, along with dilations, to produce other polynomials as required.
...
