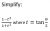-
Looking for HSC notes and resources? Check out our Notes & Resources page
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
math question help (1 Viewer)
- Thread starter SpiderX1X
- Start date
StudyOnly
Active Member
- Joined
- Oct 16, 2018
- Messages
- 171
- Gender
- Male
- HSC
- 2019
Yes you're right, just rushed the answer and forgot about θ/2.cos θ not cos 2θ