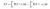-
Looking for HSC notes and resources? Check out our Notes & Resources page
MATH QUESTION HELP (1 Viewer)
- Thread starter frankfurt
- Start date
You have not written a question.Hi guys,
I’m doing ecmt3160 this semester and I’m getting stuck on this question.
View attachment 35794
Could someone please help?
Thanks in advance
What are your definition, axiom, theorems?
Are you referring to any textbook? If so have you tried using Quizlet in conjunction to a disposable email. temp mail etc
P(X>x) is just some number between 0, 1
integral_from_0_to_infinity P(X>x) - P(X<-x) dx
If X belongs to a pdf where the domain is the positive set of real numbers this will mean and x>0
P(X>x) > 0, P(X<-x) = 0.
P(X>x) = 1 - cdf(x)
Maybe this could help give you an idea. Maybe next split the integral and then use integration by parts. Of course you will need to generalise your proof for the set of real numbers
integral_from_0_to_infinity P(X>x) - P(X<-x) dx
If X belongs to a pdf where the domain is the positive set of real numbers this will mean and x>0
P(X>x) > 0, P(X<-x) = 0.
P(X>x) = 1 - cdf(x)
Maybe this could help give you an idea. Maybe next split the integral and then use integration by parts. Of course you will need to generalise your proof for the set of real numbers
I think I understood the content.Hi, thanks Cossine- your hint helped me figure it out
I had another question that I'm struggling with:
View attachment 35809
If you can please try to use (12):
View attachment 35810
Thanks in advance!
The text seems a little bit off with the wording. Instead of saying joint distribution function for definition 11 they should say joint cumulative distribution function.
https://en.wikipedia.org/wiki/Cumulative_distribution_function
So what they really want if we going by there precise wording is actually the probability mass function of X and Y. Not the cumulative probability mass function. So I am not to sure how to use 12.**
So construct 6 by 6 matrix with X on the y-axis, Y on the x-axis. This matrix is an upper diagonal matrix by definition since X <= Y. (1/6)^r is on the diagonal.
This leaves elements not on the diagonal. To find elements not on the diagonal, make use of the definition of conditional probability,
**It seems 12 only works for joint probability mass function, however the text references joint distribution functions. distribution functions include both probability density functions and probability mass functions.
thanks for your help!I think I understood the content.
The text seems a little bit off with the wording. Instead of saying joint distribution function for definition 11 they should say joint cumulative distribution function.
https://en.wikipedia.org/wiki/Cumulative_distribution_function
So what they really want if we going by there precise wording is actually the probability mass function of X and Y. Not the cumulative probability mass function. So I am not to sure how to use 12.**
So construct 6 by 6 matrix with X on the y-axis, Y on the x-axis. This matrix is an upper diagonal matrix by definition since X <= Y. (1/6)^r is on the diagonal.
This leaves elements not on the diagonal. To find elements not on the diagonal, make use of the definition of conditional probability,
**It seems 12 only works for joint probability mass function, however the text references joint distribution functions. distribution functions include both probability density functions and probability mass functions.