Maths Extension 2 predictions/thoughts? (3 Viewers)

[Drdusk]

I like the probability question

How does one like probability

 

[Idkwhattoput]

Turns out I somehow didn't see a 3 mark question. Rip. Now looking at high 80s. 97 still achievable?

 

[Jimmy.Chen]

Turns out I somehow didn't see a 3 mark question. Rip. Now looking at high 80s. 97 still achievable?

I think so. In 2013 88 got scaled to 97.

 

[Trebla]

How does one like probability

Tbf I don’t like perms/combs because I’m not the best at coming up with counting techniques but this question is not perms/combs.

The result in itself is nice using the golden ratio. Not to mention to get there it merges the concepts of probability, geometric series (if my solution to it is correct but there may be other approaches) and quadratic inequalities in the one question.

 

[hash1234]

would 70 just get me the b6 cut off? Super stressed atm

 

[Drdusk]

would 70 just get me the b6 cut off? Super stressed atm

It's cutting it pretty close. In 2018 a 72 Raw was 90 on the dot and this year seemed to be easier.

 

[danny135]

would 60 raw get me a band5???

 

[Trebla]

They went easy on the outgoing syllabus topics in this paper

 

[clbaker]

How does one like probability

How does one not?

 

[Nash__]

how long do we think for solutions??? tomorrow?

 

[brent012]

how long do we think for solutions??? tomorrow?

@sharky564 has posted some here: https://boredofstudies.org/threads/my-solutions-to-the-2019-mathematics-extension-2-paper.388915

 

[integral95]

Tbf I don’t like perms/combs because I’m not the best at coming up with counting techniques but this question is not perms/combs.

The result in itself is nice using the golden ratio. Not to mention to get there it merges the concepts of probability, geometric series (if my solution to it is correct but there may be other approaches) and quadratic inequalities in the one question.

bruh I legit got it using only 2U knowledge why is this so easy?, but yeah the final result is indeed neat

 

[psmao]

I like the probability question

Yeah I liked it but it was kinda repetitive to a 2u past hsc question 2015 iirc. U just need the limiting sum of the probability

 

[teddyboy3]

E4 cut off prediction?

 

[aa180]

For the probability question, since player 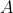starts first, player 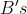chance of winning is always dependent on player 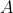failing the turn before player 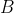selects a marble. This immediately forces the condition: . Let 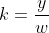and you quickly arrive at the inequality 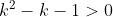, and the result follows.

 

[tywebb]

Here are solutions jointly by fun_jirachi and ruiace:

 

[Idkwhattoput]

For the probability question, since player starts first, player chance of winning is always dependent on player failing the turn before player selects a marble. This immediately forces the condition: . Let and you quickly arrive at the inequality , and the result follows.

The way I did it, was finding the probability that B wins, which is the sum of (A loses the B wins, A loses the B loses the A loses then B wins etc). Then you taking the limiting sum of this geometric series and set it greater then 1/2. The result follows.

 

[worldno17]

do yall think they'll penalise in q13 projectile for using degrees? they didn't state anything about using radians

 

[luckystrike826]

what does everyone think a 90-93 will align to? thanks

 

[大きい男]

do yall think they'll penalise in q13 projectile for using degrees? they didn't state anything about using radians

If you are given the size of an angle in radians in the question I think it is assumed that your answer will be in radians. That said, asking for a decimal approximation of an angle isnt something that lends itself to be expressed in radians, so I think you would be unlucky to be penalised.