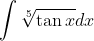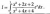He basically defined that integral as a function similar to the error function or Si(x) etc.... that isnt the integral.
am i missing something? this doesn't look like a one line answer.
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
MX2 Integration Marathon (1 Viewer)
- Thread starter dan964
- Start date
what. it looks like he diffed the integral to get what's the integrand to me.He basically defined that integral as a function similar to the error function or Si(x) etc.
Have you tried this @CM_Tutor I'm pretty sure theres an anti-derivative it's just really tricky.Ok anyone want to try this (stumped me lol):
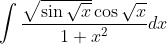
I don't see an obvious way to approach this. Integral calculator can't find an answer in elementary functions, which suggests that none of the common approaches will work. What makes you confident that there is an answer with the realm of MX2 possibilities?Ok anyone want to try this (stumped me lol):
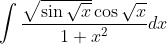
I found it on this other forum for Calc 1 (forgot where). Also I found this hint: https://math.stackexchange.com/ques...he-integral-of-sqrt-sin-sqrt-x-cos-sqrt-x-1x2I don't see an obvious way to approach this. Integral calculator can't find an answer in elementary functions, which suggests that none of the common approaches will work. What makes you confident that there is an answer with the realm of MX2 possibilities?
Not sure if that leads anywhere though
This is much tougher than I first thought as you keep running into the exponential integral,
Transforms include the denominator being a linear function of
and it cannot be expressed in elementary functions.
However, there is a closed form for this integral:
For those who want to try to solve the problem yourselves, you need to rewrite the integrand without creating terms of the form
where
You will need something of the form:
}{x+2}+\frac{g(x)}{(x+2)^2}\right)e^x)
where) and
and 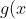) are both of degree 1.
are both of degree 1.
where
We know to leave
i.e.
I found the transformations that are suggested there, and others, but none seems to lead in a productive direction.I found it on this other forum for Calc 1 (forgot where). Also I found this hint: https://math.stackexchange.com/ques...he-integral-of-sqrt-sin-sqrt-x-cos-sqrt-x-1x2
Not sure if that leads anywhere though
That's correct. what's the hardest integration problem that you have solved?This is much tougher than I first thought as you keep running into the exponential integral,(or a transform of it), being integrals such as
Transforms include the denominator being a linear function ofor the numerator as
. Properly, the exponential integral is defined (over the complex plane) as
and it cannot be expressed in elementary functions.
However, there is a closed form for this integral:
For those who want to try to solve the problem yourselves, you need to rewrite the integrand without creating terms of the form
where,
, and
, are constants and, in this case,
or
.
You will need something of the form:
whereand
are both of degree 1.
We know to leavealone as it is clearly a problem:
i.e.is a constant plus (or minus) the exponential integral.
stupid_girl
Active Member
- Joined
- Dec 6, 2009
- Messages
- 221
- Gender
- Undisclosed
- HSC
- N/A
stupid_girl
Active Member
- Joined
- Dec 6, 2009
- Messages
- 221
- Gender
- Undisclosed
- HSC
- N/A
I made a typo in Wolfram earlier. It does give a nice answer.
e^x}{x^2+e^{2x}})
Last edited:
LetNot sure why Wolfram can't give a nice answer.
e^x}{x^2+e^{2x}})
Notice that
how come a medical student like yourself still has so much interest in math after finishing HSC?Let:
Notice thatis the derivative of
and hence the integral is in the form:
. Thus,
(using the well-known identity
)
once u learn math properly u never forget.how come a medical student like yourself still has so much interest in math after finishing HSC?
Interesting... integration calculator doesn'tI made a typo in Wolfram earlier. It does give a nice answer.
e^x}{x^2+e^{2x}})
I have a feeling @vernburn likes maths more than the stuff he is going to do in med.how come a medical student like yourself still has so much interest in math after finishing HSC?
CoolKids101
New Member
You should attend the integration bee that's being held at UNSW lolThe ultimate tedious integral:
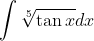
It does look like it doesn’t it! JkjkI have a feeling @vernburn likes maths more than the stuff he is going to do in med.
In reality, I really only like integration now because there is a certain elegance to it and skill required (and it’s still fresh in my head). I find the rest of maths quite boring and stale imho. My attempts at the above integrals are really just due to boredom (not long till uni starts now though).
I may be bored but not enough to attempt this monster!The ultimate tedious integral: