(Draw a diagram if you haven't already - this makes it much easier)
From the given axis (
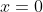
) and latus rectum (
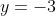
), the focus of the parabola must be
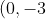 )
. (The latus rectum must pass through the focus)
Since the vertex is the origin, that means the equation of the parabola is therefore:
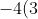y = x^2)
or
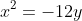
.
You can then find the equation of the required focal chord through
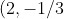 )
, which will be
x - 3)
Then you can solve this equation simultaneously with that of the parabola to obtain the other point of intersection.
You can then use Pythagoras' theorem to obtain the length of the focal chord.