-
Looking for HSC notes and resources? Check out our Notes & Resources page
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Nice proof (1 Viewer)
- Thread starter no_arg
- Start date
Let.
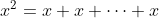
where the sum on the right has
terms.
For example ifwe have
Differentiating
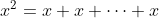
we have
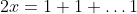
where the sum on the right still has
terms.
Thusand hence
.
Carl10101
Member
- Joined
- Aug 29, 2019
- Messages
- 40
- Gender
- Male
- HSC
- 2020
oh okhence.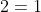
- Joined
- Feb 16, 2005
- Messages
- 8,435
- Gender
- Male
- HSC
- 2006
The main flaw is that the number of terms is also a variable whereas the additivity of differentiation applies when the number of terms is fixed. A similar example is writing:
x = 1+1+1+....+1 (x-times)
Leading to the 1 = 0 fallacy.
Another flaw is that this decomposition assumes x is an integer so obviously there are complications with limits/continuity etc.
x = 1+1+1+....+1 (x-times)
Leading to the 1 = 0 fallacy.
Another flaw is that this decomposition assumes x is an integer so obviously there are complications with limits/continuity etc.
Yeah but if you just look at the equation x+x+....+x (x times) then how can you mathematically tell that you cannot do that. Sure you can factorize it and what not to show it but that equation alone doesn't show the flaw which is weird.The main flaw is that the number of terms is also a variable whereas the additivity of differentiation applies when the number of terms is fixed. A similar example is writing:
x = 1+1+1+....+1 (x-times)
Leading to the 1 = 0 fallacy.
Another flaw is that this decomposition assumes x is an integer so obviously there are complications with limits/continuity etc.
I guess its like trying to do d/dx (x^x) as x*x^(x-1). Bcos "x times" is also varying, you can't just diff it normally.Yeah but if you just look at the equation x+x+....+x (x times) then how can you mathematically tell that you cannot do that. Sure you can factorize it and what not to show it but that equation alone doesn't show the flaw which is weird.
- Joined
- Feb 16, 2005
- Messages
- 8,435
- Gender
- Male
- HSC
- 2006
The decomposition step is perfectly valid for integer values of x.Yeah but if you just look at the equation x+x+....+x (x times) then how can you mathematically tell that you cannot do that. Sure you can factorize it and what not to show it but that equation alone doesn't show the flaw which is weird.
The invalid step is the differentiation step because it is not recognising that the number of terms is also a variable.
stupid_girl
Active Member
- Joined
- Dec 6, 2009
- Messages
- 221
- Gender
- Undisclosed
- HSC
- N/A
If the decomposition step is only valid for positive integer values of x, then it's simply not continuous and therefore not differentiatable.The decomposition step is perfectly valid for integer values of x.
The invalid step is the differentiation step because it is not recognising that the number of terms is also a variable.
I think you can have x pies but you can't have pi x's!
aren't they the same?I think you can have x pies but you can't have pi x's!
How?aren't they the same?
oh lol pies yumHow?
dan964
what
Try differentiating the RHS by first principles:
+(x+h)+\dots+(x+h)}_{(x+h) \text{ times}} - \underbrace{x+x+\dots+x}_{x \text{ times}} \right)} \\ &= \lim_{h \rightarrow 0}{\frac{1}{h}\left(\underbrace{h+h+\dots+h}_{x+h\text{ times}}+ \underbrace{x+x+\dots+x}_{h \text{ times}} \right)} \\ &= \lim_{h \rightarrow 0}{\left(\underbrace{1+1+\dots+1}_{x+h \text{ times}}+ x \right)} \\ &= \lim_{h \rightarrow 0}{2x+h} \\ &= 2x \end{align*}$$)
Last edited:
