-
Best of luck to the class of 2025 for their HSC exams. You got this! Let us know your thoughts on the HSC exams here
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Parabolas (1 Viewer)
- Thread starter Boonyak
- Start date
deswa1
Well-Known Member
- Joined
- Jul 12, 2011
- Messages
- 2,251
- Gender
- Male
- HSC
- 2012
With a lot of these, the easiest way is to graph the original function and then test a few points. For example, with y=x^2-1, it is clear that for every value of x, y=x^2-1 will be one less than y=x^2. Therefore you just shift the graph down one unit. When you do a few of them, you will be able to tell the translation very quickly...
To sketch something like x=y^3, note that it is the same thing as y=x^(1/3) so you can just sketch that.
To sketch something like x=y^3, note that it is the same thing as y=x^(1/3) so you can just sketch that.
RealiseNothing
what is that?It is Cowpea
Pretty sure you can just sketch y = x^3 then rotate it 90 degress clockwise.
SpiralFlex
Well-Known Member
- Joined
- Dec 18, 2010
- Messages
- 6,954
- Gender
- Female
- HSC
- N/A
Inverse functiiiiiiooooooonnnnnnnn
bleakarcher
Active Member
- Joined
- Jul 8, 2011
- Messages
- 1,503
- Gender
- Male
- HSC
- 2013
just reflect y=x^3 about the line y=x to obtain the graph of y=x^(1/3).
SpiralFlex
Well-Known Member
- Joined
- Dec 18, 2010
- Messages
- 6,954
- Gender
- Female
- HSC
- N/A
Note: This is posted in 2U though. They don't do inverses.
SpiralFlex
Well-Known Member
- Joined
- Dec 18, 2010
- Messages
- 6,954
- Gender
- Female
- HSC
- N/A
Some notable things, but nothing else you really need to know about this graph. Just note:
- As x values get larger, the corresponding ordinates get larger.
- Similarly as x values get smaller, the corresponding ordinates get smaller.
- There is a vertical tangent at x = 0. (This is beyond the scope of 2U)
But in 2U maths, we have found that for stationary points, the tangents will be parallel to the x axis. Hence horizontal. (Gradient 0)
What if we could find vertical tangents? Well we know a straight line parallel to the y axis has an undefined gradient, so dy/dx=undefined.


For vertical tangents, y'=undefined.

When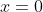 ,
, 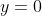
Hence there is a vertical tangent at the origin.
Now, if you were to draw this, it will be flat near the origin then diverge out very quickly! Have a go at graphing it!
- As x values get larger, the corresponding ordinates get larger.
- Similarly as x values get smaller, the corresponding ordinates get smaller.
- There is a vertical tangent at x = 0. (This is beyond the scope of 2U)
But in 2U maths, we have found that for stationary points, the tangents will be parallel to the x axis. Hence horizontal. (Gradient 0)
What if we could find vertical tangents? Well we know a straight line parallel to the y axis has an undefined gradient, so dy/dx=undefined.
For vertical tangents, y'=undefined.
When
Hence there is a vertical tangent at the origin.
Now, if you were to draw this, it will be flat near the origin then diverge out very quickly! Have a go at graphing it!
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,467
- Gender
- Undisclosed
- HSC
- N/A
Are you sure about this part?Now, if you were to draw this, it will be flat near the origin then diverge out very quickly!
If ever in doubt just test a few points. It can save you a few marks. After testing about three points you should be able to sketch the graph.
EDIT: How do you guys change from normal text to the 'natural math' text? ie what Spiral has done in the post above me.
EDIT: How do you guys change from normal text to the 'natural math' text? ie what Spiral has done in the post above me.
Last edited:
