-
Looking for HSC notes and resources? Check out our Notes & Resources page
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Pls Help Roots of Complex numbers (1 Viewer)
- Thread starter Lith_30
- Start date
note when dividing LHS by Z cubed you get:
z^3+z^-3
it is known that:
cis(nx)+cis(-nx)=2cos(nx)
Thus using this on the new LHS statement you gain, where n=3:
2cos(3 theta)
Now since you have to divide RHS by z^3, split up the division into dividing by z, 3 times. Now divide each of the brackets by z only thus:
RHS= (z+z^-1)(z-sqrt(3)+z^-1)(z+sqrt(3)+z^-1)
then collecting the applying the rule in the second line above you get:
(2cos(theta))(2cos(theta)-sqrt(3))(2cos(theta)+sqrt(3))
then taking 2 out of each of the brackets and dividing both RHS and LHS by 2 you get:
cos(3 theta) =4cos(theta)(cos(theta)-cos(pi/6))(cos(theta)+cos(5pi/6))
As required.
Thankyou! Now it makes much more sense.note when dividing LHS by Z cubed you get:
z^3+z^-3
it is known that:
cis(nx)+cis(-nx)=2cos(nx)
Thus using this on the new LHS statement you gain, where n=3:
2cos(3 theta)
Now since you have to divide RHS by z^3, split up the division into dividing by z, 3 times. Now divide each of the brackets by z only thus:
RHS= (z+z^-1)(z-sqrt(3)+z^-1)(z+sqrt(3)+z^-1)
then collecting the applying the rule in the second line above you get:
(2cos(theta))(2cos(theta)-sqrt(3))(2cos(theta)+sqrt(3))
then taking 2 out of each of the brackets and dividing both RHS and LHS by 2 you get:
cos(3 theta) =4cos(theta)(cos(theta)-cos(pi/6))(cos(theta)+cos(5pi/6))
As required.
5uckerberg
Well-Known Member
- Joined
- Oct 15, 2021
- Messages
- 561
- Gender
- Male
- HSC
- 2018
What you see here is the application of De Moivre's Theorem, and note that adding a complex number to its inverse is the same as adding a complex number to its conjugate. As such it becomes ) noting that z is the complex number. It is shown that
noting that z is the complex number. It is shown that \rightarrow{z+\frac{\bar{z}}{\bar{z}z}=z+\bar{z}}=2Re(z)) .
.
Note that the product of z and its conjugate becomes 1 as the radius is 1 if z is a general complex number
Note that the product of z and its conjugate becomes 1 as the radius is 1 if z is a general complex number
Note that the statement
 , of any modulus, like
, of any modulus, like ) , the result
, the result }) is true for all
is true for all  , but the result for
, but the result for 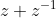 does not generalise.
does not generalise.
is true only if the complex number has a modulus of 1, for the reasons noted inWhat you see here is the application of De Moivre's Theorem, and note that adding a complex number to its inverse is the same as adding a complex number to its conjugate.
For a general complex numberIt is shown that.
Note that the product of z and its conjugate becomes 1 as the radius is 1.
5uckerberg
Well-Known Member
- Joined
- Oct 15, 2021
- Messages
- 561
- Gender
- Male
- HSC
- 2018
Thank you for demystifying my work. Sometimes there needs to be a disclaimer so that people do not get misled.Note that the statement
is true only if the complex number has a modulus of 1, for the reasons noted in
For a general complex number, of any modulus, like
, the result
is true for all
, but the result for
does not generalise.
No problem, I see part of my role as clarifying for the sake of other readers.Thank you for demystifying my work. Sometimes there needs to be a disclaimer so that people do not get misled.

