leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,768
- Gender
- Male
- HSC
- 2015
I only need the second part of part (iii). Everything else I could get out but I get something wrong for the proof.
=x^4+Ax^3+Bx^2+Ax+1\\ x=\alpha\text{ is a zero.})
 Given that }(2+B)^2\neq 4A^2\text{, show that }\alpha \neq 0, \pm 1)
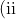 Show that }x=\frac{1}{\alpha}\text{ is a root.})
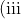 Deduce that if }\alpha\text{ is a multiple root, it has multiplicity 2 }\textbf{and this: }4B=8+A^2)
I had the four roots being alpha, alpha, 1/alpha, 1/alpha
But then I get 4B = A^2, without the eight
I had the four roots being alpha, alpha, 1/alpha, 1/alpha
But then I get 4B = A^2, without the eight
