First one:
Since it's an if and only if, we have to prove it holds both ways, this is the proof for the first way:
We know
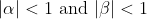
Hence we can say:
(\beta - 1) > 0)
Since each bracket individually is negative and will therefore become positive. Expanding gives:
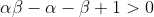
Re-arranging:
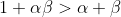
Since

We can let them equal 'c' and 'b' respectively, which by substitution gives:
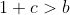
Now if both
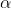
are less than 1, it follows that their sum is less than 2, and their product is less than 1, hence:
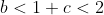
As required.
