Polynomials!?

[Currybear]

Hey, all!

I needed help with a polynomial question,

The Equation X^3 + 3x +2=0 has roots alpha ß and gamma
Find the equation with roots ß +1/ß



If possible could you do a worked solution?

 

[asianese]

Begin with the usual transformation.

Let y=x+1/x. Now solve this equation for x and then substitute this expression (in terms of y) into your original equation and you're done.

 

[Currybear]

i tried and i got a strange equation with both x and y's so i used to quad formula

then i got a +- value which is tripppin me up

if possible could you do the question on paper and send me the photo, i know its a lot to ask but it would be much obliged

 

[asianese]

Ok so you have

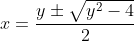which when substituted becomes



Now just consider the positive square root for now.

Multiply through by 8 to get rid of all denominators. Then use the binomial theorem to expand the first cubed bracket. Collect all the non-surd terms on one side and the surd terms on the other. Square both sides to get rid of the surd. Now simplify (lots of algebra). Do the same with the negative case (or just see where your negatives pop up and change accordingly).

 

[Currybear]

If i were to do that, i would get 2 solutions yea? but the book only has one any ideas?

and thanks heaps for your time and effort so far

 

[asianese]

Think about it. Which specific terms have the 'minus' with them (as opposed to their positive counterparts)? What will happen to these later then you square both sides to get rid of the surd?

 

[Currybear]

Think about it. Which specific terms have the 'minus' with them (as opposed to their positive counterparts)? What will happen to these later then you square both sides to get rid of the surd?

 

[cineti970128]

Begin with the usual transformation.

Let y=x+1/x. Now solve this equation for x and then substitute this expression (in terms of y) into your original equation and you're done.

asianese your method is not quite right i will tell you the right answer in approx 5 minutes

 

[asianese]

Yes. You can use the sum of roots and sum of reciprocal of roots to form a new equation. In hindsight this is easier.

 

[cineti970128]

=x^3 + 3x + 2 = 0
has roots a, b, y

therefore
1. a + b + y = 0
2. ab + ay + by = 3
3. aby = -2


Now using these identities

For the new equation coefficient of x^2

is
-(a + b + y + 1/a + 1/b + 1/y)
using simple algebra
= 3/2


coefficient of X this part is just crazy long
= (a + 1/a)(b + 1/b) + (b + 1/b)(y +1/y) + (y + 1/y)(a + 1/a)
= ab + a/b + b/a +1/ba + ay + a/y + y/a +1/by + ay + a/y + y/a +1/ya

simplifying

= (ab + by + ay) +(a+y)/b + (b+a)/y + (y+b)/a + (a + b + y)/aby

note a + b + y = 0
hence a + b = -y

=3 + (-b/b) + (-y/y) +(-a/a) +0
= 3 - 1 - 1 -1
= 0

now i am quite exhausted typing i will post the second part of answer soon

 

[cineti970128]

Now

constant
= - (a+1/a)(b+1/b)(y+1/y)
= - (aby + ab/y + ay/b + by/a + a/by + b/ay + y/ab + 1/aby)

quite long X_X

= -(-2 + -1/2 + (a^2b^2 + ......)

now i give up typing
if you re doing 4 unit you should know what to do from this step onwards

keep simplifying and you get
4

hence equation is
2x^3 + 3x^2 + 8 = 0

 

[asianese]

Both methods will work eventually. They are both as tedious.

 

[cineti970128]

if there is another way of doing it please post
although i am pretty sure that this is the best and fastest method.

Trust me you will NEVER NEVER get this question in any test

Reason
:1. too fu***** long
2. at least 3 pages of working

If it does come out, i will kill myself unless the question is like 10 mark

 

[cineti970128]

true asianese this question is just a joke

 

[cineti970128]

Yes. You can use the sum of roots and sum of reciprocal of roots to form a new equation. In hindsight this is easier.

My bad i didnt read that also the fact that the positive and negative sign does get lost
sorry X_X
Do you think this kind of question will come out in any exams?

 

[hayabusaboston]

Begin with the usual transformation.

Let y=x+1/x. Now solve this equation for x and then substitute this expression (in terms of y) into your original equation and you're done.

Perfect word hahaha :')

 

[hayabusaboston]

My bad i didnt read that also the fact that the positive and negative sign does get lost
sorry X_X
Do you think this kind of question will come out in any exams?

I had it in my exam boi.

Speaking of which, rank 1 in half yearly ext 1 maths FUCK YEA