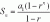Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Prelim 2016 Maths Help Thread (2 Viewers)
- Thread starter Simorgh
- Start date
- Status
- Not open for further replies.
davidgoes4wce
Well-Known Member
Do you have a diagram? Struggling a bit to visualize this one.
kawaiipotato
Well-Known Member
- Joined
- Apr 28, 2015
- Messages
- 463
- Gender
- Undisclosed
- HSC
- 2015
Here is a diagram.Don't worry, I figured both the above. But this one, idk:

http://imgur.com/b7sVG7V
Solution (highlight): Notice that the height 'd' of the building that we are required to find is just equal to 45 - x. Where x is the distance you get when you extend the top of the 2nd building to the horizontal line at the top.
x can be found using the tan ratio. tan(48 degrees 22 minutes) = x/10 ==> x = 10tan(48*22').
So the height d is just d = 45 - 10tan(48*22') = ~33.75 metres.
eyeseeyou
Well-Known Member
Need help with these questions as well as the following:More motion question for you all (this will be good for the current 3U kids):
This is motion defined by a=a(x)
1. The acceleration of particle P, moving in a straight line, is given by x (with 2 dots on top of x)=2x-3 where x metres is the displacement from the origin O. Initially the particle is at O and its velocity v is 2 metres per second
a. Show that the velocity of the particle v^2=2x^2-6x+4
b. Calculate the velocity and acceleration of P at x=1 and briefly describe the motion of P after it moves from x=1
2. The acceleration of a particle is (2x-5) m/s^2, where x in the distance in metres from the origin
a. Find an expression for the velocity of this particle in terms of x, given that the particle is at rest one metre to the left of the origin initially
b. Describe the motion
3. A particle is moving along a straight line, with velocity v m/s and acceleration given by the expression k(4-x^2) m/s^2 where k is a constant
a. Show that v^2=4+Ae^(-2kx) where A is a constant satisifies the acceleration condition
b. If it starts from x=0 with a velocity of 7m/s, find the value of A
c. Does the particle ever change direction? Justify your answer
d. At x=1, v=4m/s, find the speed correct to two decimal places when x=2
e. As the motion continues, what happens, to the velocity and acceleration
1. Find the accelertion of a particle is given by dv/dt=1-sin^2t. Initially the particle is stationary
a. Find the expression for v in terms of t
b. In which direction does the particle start to move? why?
c. Explain why the particle never comes to rest again.
3. A certain particle moves along a straight line in accordance with the law t=2x^2-5x+3, where x is measured in centimetres to the right of the origin O and moving away from O
a. Show that the velocity, v cm/s, is given by
v=1/(4x-5)
b. Find an expression for the acceleration a cm/s^2 of the particle in terms of x
c. Find the velocity and acceleration of the particle when:
i.x=2xm
ii. t=6 seconds
d. Describe carefully in words the motion of the particle
eyeseeyou
Well-Known Member
BTW these q's are x,v,t equationsNeed help with these questions as well as the following:
1. Find the accelertion of a particle is given by dv/dt=1-sin^2t. Initially the particle is stationary
a. Find the expression for v in terms of t
b. In which direction does the particle start to move? why?
c. Explain why the particle never comes to rest again.
3. A certain particle moves along a straight line in accordance with the law t=2x^2-5x+3, where x is measured in centimetres to the right of the origin O and moving away from O
a. Show that the velocity, v cm/s, is given by
v=1/(4x-5)
b. Find an expression for the acceleration a cm/s^2 of the particle in terms of x
c. Find the velocity and acceleration of the particle when:
i.x=2xm
ii. t=6 seconds
d. Describe carefully in words the motion of the particle
Thanks in advance
Need help with these questions as well as the following:
1. Find the accelertion of a particle is given by dv/dt=1-sin^2t. Initially the particle is stationary
a. Find the expression for v in terms of t
b. In which direction does the particle start to move? why?
c. Explain why the particle never comes to rest again.
3. A certain particle moves along a straight line in accordance with the law t=2x^2-5x+3, where x is measured in centimetres to the right of the origin O and moving away from O
a. Show that the velocity, v cm/s, is given by
v=1/(4x-5)
b. Find an expression for the acceleration a cm/s^2 of the particle in terms of x
c. Find the velocity and acceleration of the particle when:
i.x=2xm
ii. t=6 seconds
d. Describe carefully in words the motion of the particle
1(b) When t = 0, the particle experiences acceleration = 1-sin^2(0) = 1, which is positive and the particle is stationary initially (meaning it doesn't have negative velocity at t=0). So the particle with start moving to the right initially (i.e. in the positive direction)
Last edited:
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,794
- Gender
- Male
- HSC
- 2015
Q3 requires a bit of Ext 1Need help with these questions as well as the following:
1. Find the accelertion of a particle is given by dv/dt=1-sin^2t. Initially the particle is stationary
a. Find the expression for v in terms of t
b. In which direction does the particle start to move? why?
c. Explain why the particle never comes to rest again.
3. A certain particle moves along a straight line in accordance with the law t=2x^2-5x+3, where x is measured in centimetres to the right of the origin O and moving away from O
a. Show that the velocity, v cm/s, is given by
v=1/(4x-5)
b. Find an expression for the acceleration a cm/s^2 of the particle in terms of x
c. Find the velocity and acceleration of the particle when:
i.x=2xm
ii. t=6 seconds
d. Describe carefully in words the motion of the particle
____
____
Part iii should be obvious.
____
eyeseeyou
Well-Known Member
How do I draw graphs here?
Also
1. Car A and car B are travelling along a straight level road at constant speeds Va and Vb respectively. Car A is behind car B, but is travelling faster
When car A is exactly D metres behind car B, car A applies its brakes, producing a constant deceleration of k m/s^2
a. Using calculus, find the speed of the car A after it has travelled a distance x metres under breaking
b. Prove that the cars will collide if Va-Vb is greater than squareroot of (2kD)
2. A position moving in a straight line has an acceleration of (8t-2)m/s^2. The particle passes through the origin with a velocity of 2 m/s in the negative direction two seconds after observations commenced:
a. Find expression for its positions and velocity at time, t
b. When will the particle next pass through the origin? give your answer correct to two decimal places
3. Two particle P and Q move along a line, their displacement at time t with respect to a fixed point O being x(t) and X(t), respectively.
a. The acceleration of P is given by d^2x/dt^2=6+e^(-t). If it begins its motion at x=0 with a velocity of -1, find an expression for x(t)
b. If X(t)=2sin5t+3t^2+2, prove that X(t)>x(t) for all t is greater or equal to 0
Also
1. Car A and car B are travelling along a straight level road at constant speeds Va and Vb respectively. Car A is behind car B, but is travelling faster
When car A is exactly D metres behind car B, car A applies its brakes, producing a constant deceleration of k m/s^2
a. Using calculus, find the speed of the car A after it has travelled a distance x metres under breaking
b. Prove that the cars will collide if Va-Vb is greater than squareroot of (2kD)
2. A position moving in a straight line has an acceleration of (8t-2)m/s^2. The particle passes through the origin with a velocity of 2 m/s in the negative direction two seconds after observations commenced:
a. Find expression for its positions and velocity at time, t
b. When will the particle next pass through the origin? give your answer correct to two decimal places
3. Two particle P and Q move along a line, their displacement at time t with respect to a fixed point O being x(t) and X(t), respectively.
a. The acceleration of P is given by d^2x/dt^2=6+e^(-t). If it begins its motion at x=0 with a velocity of -1, find an expression for x(t)
b. If X(t)=2sin5t+3t^2+2, prove that X(t)>x(t) for all t is greater or equal to 0
eyeseeyou
Well-Known Member
Thanks m8Q3 requires a bit of Ext 1
____
____
Part iii should be obvious.
____

Really appreciated (for someone like you to help someone as annoying as me lol)
any formal way of proving this?
Prove f(x) = 1 + x + x^2 ... + x^(2n -1) + x^(2n) is always positive
did one, but not sure if right
Notice that this is a geometric series with factor r = x, first term a = 1 and has 2n terms: Chuck this into the formulaany formal way of proving this?
Prove f(x) = 1 + x + x^2 ... + x^(2n -1) + x^(2n) is always positive
did one, but not sure if right

And yeah you got yourself a formal proof!
Attachments
-
1.1 KB Views: 98
Guess InteGrand beat me to it lol
eyeseeyou
Well-Known Member
Can someone help me?How do I draw graphs here?
Also
1. Car A and car B are travelling along a straight level road at constant speeds Va and Vb respectively. Car A is behind car B, but is travelling faster
When car A is exactly D metres behind car B, car A applies its brakes, producing a constant deceleration of k m/s^2
a. Using calculus, find the speed of the car A after it has travelled a distance x metres under breaking
b. Prove that the cars will collide if Va-Vb is greater than squareroot of (2kD)
2. A position moving in a straight line has an acceleration of (8t-2)m/s^2. The particle passes through the origin with a velocity of 2 m/s in the negative direction two seconds after observations commenced:
a. Find expression for its positions and velocity at time, t
b. When will the particle next pass through the origin? give your answer correct to two decimal places
3. Two particle P and Q move along a line, their displacement at time t with respect to a fixed point O being x(t) and X(t), respectively.
a. The acceleration of P is given by d^2x/dt^2=6+e^(-t). If it begins its motion at x=0 with a velocity of -1, find an expression for x(t)
b. If X(t)=2sin5t+3t^2+2, prove that X(t)>x(t) for all t is greater or equal to 0
apparently my friend got that q from functions chapter 3 from Cambridge 3u yr11. Which is before series and sequence. But looking at it now, it has walkthrough questions before that, sorry about that haha. Thanks both
- Status
- Not open for further replies.