Shadia has invented a game for one person. she throws two dice repeatedly until the sum of the two numbers shown is either six or eight. if the sum is six, she wins. if the sum is eight, she loses. if the sum is any other number, she continues to throw until the sum is six or eight. calculate the probability that Shadia wins the gameHey
-
Looking for HSC notes and resources? Check out our Notes & Resources page
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Probability question please help (1 Viewer)
- Thread starter kpad5991
- Start date
Shadia has invented a game for one person. she throws two dice repeatedly until the sum of the two numbers shown is either six or eight. if the sum is six, she wins. if the sum is eight, she loses. if the sum is any other number, she continues to throw until the sum is six or eight. calculate the probability that Shadia wins the gameHey
The solution in the book is 1/2??Firstly Integrand....... 4 AM mafffsss
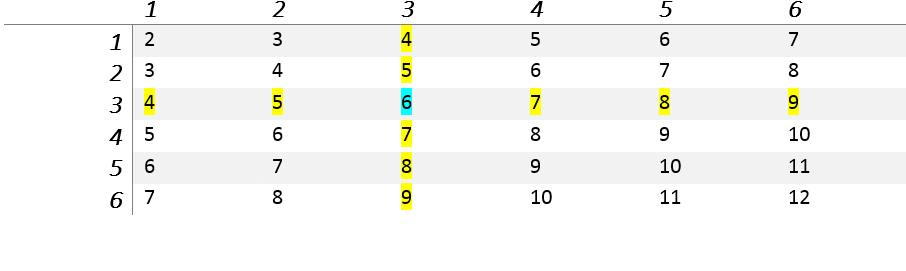
pls ignore thr higlights.
Anyway.
} = \bigg(\frac{25}{36} \bigg) \bigg(\frac{5}{36} \bigg) = \bigg(\frac{125}{1296} \bigg))
} = \bigg(\frac{25}{36} \bigg)\bigg(\frac{25}{36} \bigg) \bigg(\frac{5}{36} \bigg) = \bigg(\frac{3125}{56656} \bigg) )
}{1-\bigg(\frac{25}{36}\bigg)} = \frac{5}{11} )
Okay I figured it out. Shadia continues for 26/36The solution in the book is 1/2??
kawaiipotato
Well-Known Member
- Joined
- Apr 28, 2015
- Messages
- 462
- Gender
- Undisclosed
- HSC
- 2015
Just a note that you should expect 1/2 because the number of desired outcomes are equal in both cases.The solution in the book is 1/2??
KAIO7
Member
You've made a silly mistake in evaluating the probability of continuing the game; it should be 26/36 instead of 25/36. When using this, the limiting sum will be equal to 1/2, hence the probability of winning the game is 1/2
Last edited:
