okay I'll assume you mean prove 2
n < 3
n.
First note that you don't need induction to prove this – you can simply raise both sides of 2 < 3 to the power of n (as both sides are greater than zero & x
n is strictly increasing for x > 0).
However, using induction:
1. The base case is obvious as 2
1 < 3
1.
2. Let the induction hypothesis be 2
k < 3
k for some integer k.
3. Consider
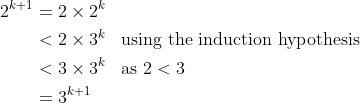
Therefore the statement is true for all positive integers n.
Induction with inequalities can be difficult. I suppose it's just practise..
Become familiar with rules of inequalities and ways you can get the answer, e.g., in this example we needed to get a 3 from 2, so we used 2 < 3. You can do the same with things such as n < n + 1, n < 2n (n > 0), etc.
You might find it easier to prove LHS - RHS > 0 and conclude that LHS > RHS.
If you have any further questions feel free to ask.

