-
Finished your HSC? Check out our University Discussion, Non-School forums or help out next year's HSC students! -
YOU can help the next generation of students in the community! Share your trial papers and notes on our Notes & Resources page
Rates 3 Unit (1 Viewer)
- Thread starter Pedro123
- Start date
First, note that this is quite an improbable situation: 
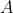
and 
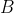
on perfectly level (horizontal) ground such that the vertical plane containing 
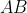
also includes 
and 
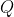
... and thus the plane is travelling directly towards both and .
Nevertheless, accepting this as a model, we can rearrange before differentiating. Taking the result from part (a):
 \tan \alpha \\ x\tan \beta &= x \tan \alpha + 100 \tan \alpha \\ x(\tan \beta - \tan \alpha) &= 100 \tan \alpha \end{align*})
Now, as
, 
, and 
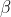
are all functions of 
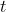
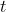
, we can implicitly differentiate with respect to . In so doing, we will use the "dot notation" convention, which says that 
, 
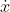
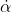
, and 
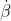
are alternative ways to write (respectively) the time derivatives 
, 
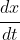
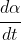
, and 
.
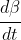
\Big) &= \cfrac{d}{dt} \Big(100 \tan \alpha\Big) \\ \big(\tan \beta - \tan \alpha\big)\cfrac{dx}{dt} + x\cfrac{d}{dt}\big(\tan \beta - \tan \alpha\big) &= 100\cfrac{d}{dt} \tan \alpha \\ \dot{x}\big(\tan \beta - \tan \alpha\big) + x\bigg(\cfrac{d}{d\beta} \tan \beta \times \cfrac{d\beta}{dt} - \cfrac{d}{d\alpha} \tan \alpha \times \cfrac{d\alpha}{dt}\bigg) &= 100\cfrac{d}{d\alpha} \tan \alpha \times \cfrac{d\alpha}{dt} \\ \dot{x}\big(\tan \beta - \tan \alpha\big) + x\big(\sec^2 \beta \times \dot{\beta} - \sec^2 \alpha \times \dot{\alpha}\big) &= 100\sec^2 \alpha \times \dot{\alpha} \\ \dot{x}\big(\tan \beta - \tan \alpha\big) &= 100\dot{\alpha}\sec^2 \alpha - x\big(\dot{\beta}\sec^2 \beta - \dot{\alpha}\sec^2 \alpha\big) \\ \dot{x} = \cfrac{dx}{dt} &= \cfrac{\dot{\alpha}(100 + x)\sec^2 \alpha - x\dot{\beta}\sec^2 \beta}{\tan \beta - \tan \alpha} \end{align*})
Nevertheless, accepting this as a model, we can rearrange before differentiating. Taking the result from part (a):
Now, as