asianese
Σ
- Joined
- Sep 20, 2010
- Messages
- 2,219
- Gender
- Undisclosed
- HSC
- 2012
(a) (i) 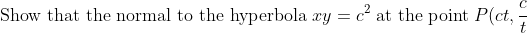 \\\;\text{has equation} \;ty-t^3x=c(1-t^4).) (2 marks)
(2 marks)
(ii) \;\text{on the y-axis, exactly two normals can be drawn to the hyperbola.}) (4 marks)
(4 marks)
(iii) Show that there can never be more than four normals drawn to the hyperbola from an arbitrary point in the plane. (1 mark)
I've done 1 (trivial). Struggling for ii and iii. Do we solve the point with the normal?? Leads to nothing...
Any help is appreciated.
(ii)
(iii) Show that there can never be more than four normals drawn to the hyperbola from an arbitrary point in the plane. (1 mark)
I've done 1 (trivial). Struggling for ii and iii. Do we solve the point with the normal?? Leads to nothing...
Any help is appreciated.


