asianese
Σ
- Joined
- Sep 20, 2010
- Messages
- 2,219
- Gender
- Undisclosed
- HSC
- 2012
It is a common question, I've seen it 2 times in papers...I can't seem to get the last part. I know that I need to times top/bottom by other terms but not sure. Any help is appreciated. Don't worry about latex, a method is just as good =D Thanks
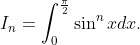

!}{2^{2n+1}{(n!)^2}})
I've got i) easily, but the 2nd part..hmm. I've expanded and tried a couple of things but didn't work.
I've got i) easily, but the 2nd part..hmm. I've expanded and tried a couple of things but didn't work.
Last edited:
