Could some capable person please tell me how to solve this?
_______________________________________________
A point "P" moves on the curve y=x^3 and its x-coordinate increases at a constant rate of 5 units per second.
At what rate is the gradient of the curve increasing when x=1?
_______________________________________________
Answer (highlight to see): 30 units/s
OMG, it has been 9 years since i have done Math like this, but i will try

So, we know the following:
1. y = x^3
2. rate at which x-co ord increases (i.e., dx/dt) = 5 units/sec
We want the rate at which the gradient increases, which is essentially (dy/dx)/dt
So:
from 1. dy/dx = 3x^2
we want (dy/dx)/dt
so (dy/dx)/dt = dy/dx * 1/dt
dx/dt = 5, so
1/dt = 5/dx --- sub into previous
so (dy/dx)/dt = dy/dx *
1/dt
(dy/dx)/dt = 3x^2 * (5/dx)
(dy/dx)/dt = 15x^2 * (1/dx)
(dy/dx)/dt = 15x^2/dx
(dy/dx)/dt = 30x
when x = 1
(dy/dx)/dt = 30*1
(dy/dx)/dt = 30

Sorry folks, here's another one. Several times I've tried and gotten 96 as opposed to 288.
Q: Sand is poured into a heap in the shape of a right circular cone whose semi-vertex angle is A, where
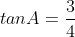
. When the height of the cone is 16cm, the height is increasing at the rate of 2cm/min. At what rate is the volume increasing at that instant?
Answer: 288pi
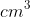
/min
Just quickly looking at this. If you got 96 and answer is 288. Odds are they used the wrong formula for volume of a cone, they probably left out the 1/3 part

dV/dt = dh/dt * dV/dh
dV/dt = 2 * 1/3(pi)r^2
dV/dt = 2 * 1/3(pi)(16*3/4)^2
dV/dt = 2/3(pi)(12)^2
dV/dt = 288/3 (pi)
dV/dt = 96pi

