Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Simultaneous Parabola (1 Viewer)
- Thread starter Lukybear
- Start date
tangent to parabola = gradient is negetive reciprical of the eqn y = x^2-2x+5 .
Once you have the negetive reciprical, plug the points + gradient into the : point gradient formula
y-y1= m(x-x1)
this may not be 100% correct so prob. ask someone else too
Once you have the negetive reciprical, plug the points + gradient into the : point gradient formula
y-y1= m(x-x1)
this may not be 100% correct so prob. ask someone else too
ninetypercent
ninety ninety ninety
dy/dx = 2x - 2




 = 0 )
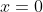 or
or 
dy/dx = 2x - 2
when x = 0, m = -2



when x = 2, m = 2



I think... this must be wrong
dy/dx = 2x - 2
when x = 0, m = -2
when x = 2, m = 2
I think... this must be wrong
untouchablecuz
Active Member
- Joined
- Mar 25, 2008
- Messages
- 1,693
- Gender
- Male
- HSC
- 2009
the tangent is in the form:
y=mx+b
solving simultaneously with y=x^2-2x+5
x^2-(m+2)x+(5-b)
discriminant = 0 since the line is tangent and there is only 1 point of contact
i.e. (m+2)^2-4(5-b)=0 => m^2+4m-16+4b=0 [1]
(1,3) satisfies y=mx+b since it passes through it
i.e. 3=m+b => b=3-m [2]
sub [2] in [1]
m^2-4=0
m= 2 or -2
from [2] b = 1 or 5
hence,
y=2x+1 and y=-2x+5 are the tangents
y=mx+b
solving simultaneously with y=x^2-2x+5
x^2-(m+2)x+(5-b)
discriminant = 0 since the line is tangent and there is only 1 point of contact
i.e. (m+2)^2-4(5-b)=0 => m^2+4m-16+4b=0 [1]
(1,3) satisfies y=mx+b since it passes through it
i.e. 3=m+b => b=3-m [2]
sub [2] in [1]
m^2-4=0
m= 2 or -2
from [2] b = 1 or 5
hence,
y=2x+1 and y=-2x+5 are the tangents
untouchablecuz
Active Member
- Joined
- Mar 25, 2008
- Messages
- 1,693
- Gender
- Male
- HSC
- 2009
anytime my man
anytimeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeee
anytimeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeee
