Surface Area question please show working (1 Viewer)

[kpad5991]

 

[Eagle Mum]

Given that the triangles with base length of 7mm are right angled triangles, the back triangle is a vertical face of this pyramid (ie. perpendicular to the ground) and the vertical height of the pyramid is 24 mm. This can also be confirmed by recognising the Pythagorean triads, 7,24,25: 24^2 + 7^2 = 25^2

The slope height of the small triangles (the edge between the back face and the face with base of 7 mm) can be calculated by another Pythagorean equation:
h^2 = 24^2 + (36/2)^2 = 900
h = 30

Therefore the surface areas of the faces are (noting the area of each triangular face = h x b/2):

2x(30x7/2) + 25x36/2 + 24x36/2 + 36x7
= 210 + 450 + 432 + 252 = 1344 mm^2

 

[CM_Tutor]

Was any other information given, other than the diagram? @Eagle Mum's solution appears correct to me (I haven't checked the calculator work at the end), but it rests on the assumption that the base is a rectangle (needed for its area to be 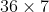) and so that the 24 mm and 25 mm altitudes of two of the faces are coplanar and bisect their respective bases, also making the two small faces are congruent triangles and identical in area. I am wondering if the question addressed these details, or if you need to explicitly make the assumption of a rectangular base

 

[kpad5991]

Given that the triangles with base length of 7mm are right angled triangles, the back triangle is a vertical face of this pyramid (ie. perpendicular to the ground) and the vertical height of the pyramid is 24 mm. This can also be confirmed by recognising the Pythagorean triads, 7,24,25: 24^2 + 7^2 = 25^2

The slope height of the small triangles (the edge between the back face and the face with base of 7 mm) can be calculated by another Pythagorean equation:
h^2 = 24^2 + (36/2)^2 = 900
h = 30

Therefore the surface areas of the faces are (noting the area of each triangular face = h x b/2):

2x(30x7/2) + 25x36/2 + 24x36/2 + 36x7
= 210 + 450 + 432 + 252 = 1344 mm^2

Thank you so much

 

[Eagle Mum]

@CM_Tutor, I did consider the diagram, who posted the question and the section in which it was posted. I was a bit unsure about the details of the former (date joined), but decided that this section of the forum is for students in Yrs 9-10 (incidentally the stage my 13 yr old is currently in) and the content of the stage 5 curriculum for volume & surface area of pyramids is quite straightforward, the ‘twist’ in this question being that the back triangle is a vertical face and therefore that the vertical height and slope height are the same.

 

[Eagle Mum]

This is beyond the stage 5 curriculum, but it is interesting to explore the constraints on the 3D shape if the base were a non rectangular parallelogram which provides an insight on how questions are created.

Firstly, without other given measurements for the back edges to suggest otherwise, one can only proceed with the presumption that the base is at least a parallelogram.

Using an (x,y,z) coordinate system, let‘s nominate the back corner of the base as the origin and the back base edge the line from (0,0,0) to (0,0,18), then the parallel side is a line from (W,0,Z) to (W,0,Z+18) where 0<W<7. If it were a regular acute pyramid (ie. apex of the pyramid lies above the base of the pyramid) then the apex coordinates (A,H,R) are thus constrained 0<A<W<7 and 0<H<24. By definition, the perpendicular line from the apex, of length 24 mm, intersects the back base edge at (0,0,R). Similarly, the perpendicular line from the apex, of length 25 mm, intersects the opposite base edge at (W,0,R). Both these points of intersection, both perpendicular lines and the apex all lie on the plane defined by z=R and are therefore co-planar (note these are co-planar if the base is a parallelogram, whether or not it is rectangular).

Thus, we have the cross sectional triangle comprised of this apex, perpendicular slopes to the edges of the base and perpendicular line across the base with respective side lengths of 24, 25 and ‘<7’ mm. By the cosine rule, to calculate the angle opposite the longest side: cos θ = - (25^2 - (24^2 + W^2)) / 48W

If, as required in a non-rectangular parallelogram, 0 < W < 7, then cos θ < 0 and θ > 90 degrees (not acute). Therefore, if the base is a non rectangular parallelogram with the given measurements, then the shape must be an obtuse pyramid where the apex lies outside of the perimeter of the base. If W = 7, then cos θ = 0 and θ = 90 degrees and the pyramid’s back face would be a vertical face (a right angled pyramid as per my original post) and since, in this case, the perpendicular distance between the longer pair of parallel sides equals the length of the shorter sides, the base must therefore be a rectangle (without the need for an explicit label). Since W can be neither negative nor exceed the length of the shortest sides of the base (7 mm), with its given dimensions, this pyramid cannot be acute.

It is often handy to recognise Pythagorean triads and other known connections between numbers as you can immediately reverse engineer and see how questions were constructed.