1) A cuboid of length 5 m, breadth 3 m and depth 2 m required 4 tins of paint to give it three coats. How many tins of paint would be needed to give three coats of paint to a cuboid whose dimensions are doubled?
2) A rectangular prism has a Volume V. A second rectangular prism with edges twice the length of the edges of the first, has a volume which differs from that of the first prism by:
A) V
B) 3V
C) 5V
D) 7V
3) A hollow cylinder, open at one end and closed at the other, has a length of b cm and a base radius of r cm. If it is to be painted both inside and outside, the painted area to be covered is:

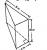
4) The volume of the right prism below is
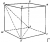
5) The cube has edges 10 cm long. Calculate the volume of the pyramid PWXZ
2) A rectangular prism has a Volume V. A second rectangular prism with edges twice the length of the edges of the first, has a volume which differs from that of the first prism by:
A) V
B) 3V
C) 5V
D) 7V
3) A hollow cylinder, open at one end and closed at the other, has a length of b cm and a base radius of r cm. If it is to be painted both inside and outside, the painted area to be covered is:

4) The volume of the right prism below is

5) The cube has edges 10 cm long. Calculate the volume of the pyramid PWXZ

